
【题目】在△ABC中,∠C>∠B,AE平分∠BAC,F为射线AE上一点(不与点E重合),且FD⊥BC于D;
(1)如果点F与点A重合,且∠C=50°,∠B=30°,如图1,求∠EFD的度数; 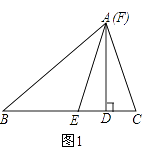
(2)如果点F在线段AE上(不与点A重合),如图2,问∠EFD与∠C﹣∠B有怎样的数量关系?并说明理由. 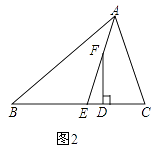
(3)如果点F在△ABC外部,如图3,此时∠EFD与∠C﹣∠B的数量关系是否会发生变化?请说明理由. 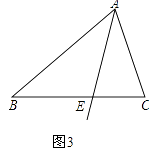
【答案】
(1)解:∵∠C=50°,∠B=30°,
∴∠BAC=180°﹣50°﹣30°=100°.
∵AE平分∠BAC,
∴∠CAE=50°.
在△ACE中∠AEC=80°,
在Rt△ADE中∠EFD=90°﹣80°=10°
(2)解:∠EFD= ![]() (∠C﹣∠B)
(∠C﹣∠B)
证明:∵AE平分∠BAC,
∴∠BAE= ![]() =90°﹣
=90°﹣ ![]() (∠C+∠B)
(∠C+∠B)
∵∠AEC为△ABE的外角,
∴∠AEC=∠B+90°﹣ ![]() (∠C+∠B)=90°+
(∠C+∠B)=90°+ ![]() (∠B﹣∠C)
(∠B﹣∠C)
∵FD⊥BC,
∴∠FDE=90°.
∴∠EFD=90°﹣90°﹣ ![]() (∠B﹣∠C)
(∠B﹣∠C)
∴∠EFD= ![]() (∠C﹣∠B)
(∠C﹣∠B)
(3)解:∠EFD= ![]() (∠C﹣∠B).
(∠C﹣∠B).
如图,
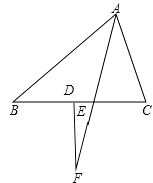
∵AE平分∠BAC,
∴∠BAE= ![]() .
.
∵∠DEF为△ABE的外角,
∴∠DEF=∠B+ ![]() =90°+
=90°+ ![]() (∠B﹣∠C),
(∠B﹣∠C),
∵FD⊥BC,
∴∠FDE=90°.
∴∠EFD=90°﹣90°﹣ ![]() (∠B﹣∠C)
(∠B﹣∠C)
∴∠EFD= ![]() (∠C﹣∠B)
(∠C﹣∠B)
【解析】(1)由三角形内角和定理可得∠BAC=100°,∠CAD=40°,由角平分线的性质易得∠EAC的度数,可得∠EFD;(2)由角平分线的性质和三角形的内角和得出∠BAE=90°﹣ ![]() (∠C+∠B),外角的性质得出∠AEC=90°+
(∠C+∠B),外角的性质得出∠AEC=90°+ ![]() (∠B﹣∠C),在△EFD中,由三角形内角和定理可得∠EFD;(3)与(2)的方法相同.
(∠B﹣∠C),在△EFD中,由三角形内角和定理可得∠EFD;(3)与(2)的方法相同.
【考点精析】本题主要考查了三角形的内角和外角和三角形的外角的相关知识点,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角;三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某商场为做好“家电下乡”的惠民服务,决定从厂家购进甲、乙、丙三种不同型号的电视机108台,其中甲种电视机的台数是丙种的4倍,购进三种电视机的总金额不超过147 000元,已知甲、乙、丙三种型号的电视机的出厂价格分别为1 000元/台,1 500元/台,2 000元/台.
(1)求该商场至少购买丙种电视机多少台?
(2)若要求甲种电视机的台数不超过乙种电视机的台数,问有哪些购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
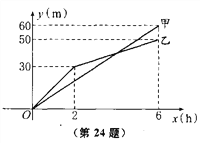
【题目】甲、乙两个工程队分别同时开始挖两段河渠,所挖河渠的长度与挖掘时间之间的关系如图所示,请根据图象所提供的信息解答下列问题:
(1) 乙队开挖到30 m时,用了 h ;开挖6 h,甲队比乙队多挖了 m ;
(2) 请你求出: ①甲队在2≤![]() ≤6的时段内,y与
≤6的时段内,y与![]() 之间的函数关系式;
之间的函数关系式;
②乙队在2≤![]() ≤6的时段内,y与
≤6的时段内,y与![]() 之间的函数关系式.
之间的函数关系式.
(3) ![]() 的取值在什么范围内时,甲工程队挖的河渠的长度比乙工程队所挖河渠的长度长?
的取值在什么范围内时,甲工程队挖的河渠的长度比乙工程队所挖河渠的长度长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国是世界上严重缺水的国家之一.为了增强居民节水意识.某市自来水公司对居民用水采用以户为单位分段汁费办法收费.即一月用水10 t以内(包括10 t)的用户.每吨收水费a元,一月用水超过10 t的用户,10 t水仍按每吨a元收费,超过10 t的部分,按每吨b元(b>a)收费.设一户居民月用水x(t),应缴水费y(元).y与x之间的函数关系如图所示.
(1)求a的值,某户居民上月用水8 t.应收水费多少元?
(2)求b的值,并写出当x>10时.y与x之间的函数关系式;
(3)已知居民甲上月比居民乙多用水4 t.两家共收消费46元.求他们上月分别用水多少吨?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人共同解方程组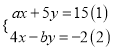 ,由于甲看错了方程①中的a,得到方程组的解为
,由于甲看错了方程①中的a,得到方程组的解为![]() 乙看错了方程②中的b,得到方程组的解为
乙看错了方程②中的b,得到方程组的解为![]() ,试计算a2015+(﹣
,试计算a2015+(﹣![]() b)2016.
b)2016.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2)
(1)求直线AB的表达式
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列统计活动中不适宜用问卷调查的方式收集数据的是( )
A.某停车场中每天停放的蓝色汽车的数量
B.七年级同学家中电视机的数量
C.每天早晨同学们起床的时间
D.各种手机在使用时所产生的辐射
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,且抛物线经过A(-1,0),C(0,-5)两点,与x轴交于点B.
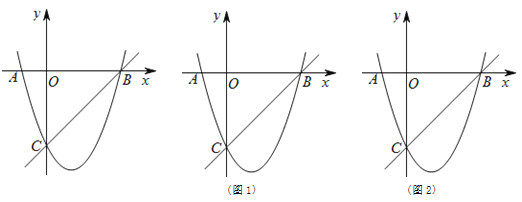
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)设点P为抛物线上的一个动点,连接PB、PC,若△BPC是以BC为直角边的直角三角形,求此时点P的坐标;
(3)在抛物线上BC段有另一个动点Q,以点Q为圆心作⊙Q,使得⊙Q与直线BC相切,在运动的过程中是否存在一个最大⊙Q. 若存在,请直接写出最大⊙Q的半径;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com