
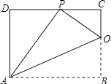
【题目】已知矩形ABCD的一条边AD=8,将矩形ABCD折叠,使得顶点B落在CD边上的P点处.如图,已知折痕与边BC交于O,连结AP、OP、OA.
①求证:△OCP∽△PDA;
②若△OCP与△PDA的面积比为1:4,求边AB的长.
【答案】(1)见试题解析;(2)AB的长为10.
【解析】
试题分析:①只需证明两对对应角分别相等即可证到两个三角形相似;
②根据相似三角形的性质求出PC长以及AP与OP的关系,然后在Rt△PCO中运用勾股定理求出OP长,从而求出AB长.
试题解析:①∵四边形ABCD是矩形,
∴AD=BC,DC=AB,∠DAB=∠B=∠C=∠D=90°.
由折叠可得:AP=AB,PO=BO,∠PAO=∠BAO,∠APO=∠B.
∴∠APO=90°.
∴∠APD=90°﹣∠CPO=∠POC.
∵∠D=∠C,∠APD=∠POC.
∴△OCP∽△PDA.
②∵△OCP与△PDA的面积比为1:4,∴![]() =
=![]() =
=![]() .
.
∴PD=2OC,PA=2OP,DA=2CP.∵AD=8,∴CP=4,BC=8.
设OP=x,则OB=x,CO=8﹣x.
在Rt△PCO中,
∵∠C=90°,CP=4,OP=x,CO=8﹣x,
∴x2=(8﹣x)2+42.
解得:x=5.
∴AB=AP=2OP=10.
∴边AB的长为10.


科目:初中数学 来源: 题型:
【题目】2016年某市用于资助贫困学生的助学金总额是9680000元,将9680000用科学记数法表示为( )
A. 96.8×105 B. 9.68×106 C. 9.68×107 D. 0.968×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解方程:x2-4x+2=0,下列配方正确的是( )
A.(x-2)2=2 B.(x+2)2=2 C.(x-2)2=-2 D.(x-2)2=6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个两位数x和一个三位数y,若将两位数x放在三位数y的左边组成一个五位数,则组成的这个五位数表示为( )
A. xy B. 10000x+y C. 100x+1000y D. 1000x+y
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,△OBC的顶点分别为O(0,0),B(3,﹣1)、C(2,1).
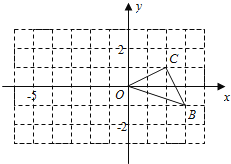
(1)以点O(0,0)为位似中心,按比例尺2:1在位似中心的异侧将△OBC放大为△OB′C′,放大后点B、C两点的对应点分别为B′、C′,画出△OB′C′,并写出点B′、C′的坐标:B′( , ),C′( , );
(2)在(1)中,若点M(x,y)为线段BC上任一点,写出变化后点M的对应点M′的坐标( , ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com