
【题目】如图,![]() 是正三角形
是正三角形![]() 内的一点,且
内的一点,且![]() ,
,![]() ,
,![]() .若将
.若将![]() 绕点
绕点![]() 逆时针旋转60°后,得到
逆时针旋转60°后,得到![]() ,则
,则![]() ________.
________.

【答案】150°
【解析】
根据旋转的性质得到∠PAP′=60°,PA=P′A=6,P′B=PC=10,利用等边三角形的判定方法得到△PAP′为等边三角形,再根据等边三角形的性质有PP′=PA=6,∠P′PA=60°,由于PP′2+PB2=P′B2,根据勾股定理的逆定理得到△BPP′为直角三角形,且∠BPP′=90°,则∠APB=∠P′PA+∠BPP′=60°+90°=150°.
∵△PAC绕点A逆时针旋转60°后,得到△P′AB,
∴∠PAP′=60°,PA=P′A=6,P′B=PC=10,
∴△PAP′为等边三角形,
∴PP′=PA=6,∠P′PA=60°,
在△BPP′中,P′B=10,PB=8,PP′=6,
∵62+82=102,
∴PP′2+PB2=P′B2,
∴△BPP′为直角三角形,且∠BPP′=90°,
∴∠APB=∠P′PA+∠BPP′=60°+90°=150°.
故答案为:150°


科目:初中数学 来源: 题型:
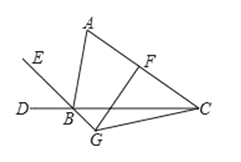
【题目】如图 ,BE平分△ABC的外角∠ABD,F是 AC的中点,过 F点作 AC的垂线交 BE的反向延长线于 G点, 连 EG.若∠ABC=80°,则∠ACG的度数为是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把边长为1厘米的6个相同正方体摆成如图的形式.

(1)该几何体的表面积为___________![]() ;
;
(2)如果在这个几何体上再添加一些相同的小正方体,使得从上面和从左面看到的图形保持不变,那么最多可以再添加__________个小正方体,并在下面的方格纸中画出添加小正方体后你从正面所看到的几何体形状图(画出符合条件中的一种即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=3a2b﹣2ab2+abc,B=﹣2a2b+ab2+2abc.
(1)求2A﹣B;
(2)小强同学说:“当c=﹣2018时和c=2018时,(1)中的结果都是一样的”,你认为对吗?说明理由;
(3)若a=![]() ,b=
,b=![]() ,求2A﹣B的值.
,求2A﹣B的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
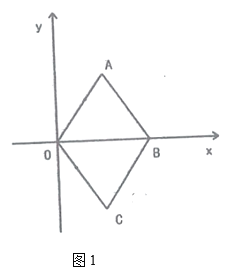
【题目】四边形![]() 是菱形,
是菱形,![]() ,
,![]()
(1)如图1,作![]() 的平分线
的平分线![]() ,交
,交![]() 于
于![]() (不写作法和证明,保留作图痕迹)
(不写作法和证明,保留作图痕迹)
(2)在(1)的条件下,点![]() 在直线
在直线![]() 上,
上,![]() 最大值时,求
最大值时,求![]() 的长
的长
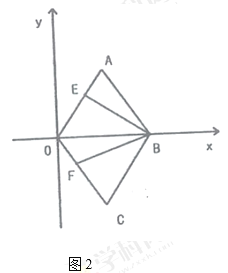
(3)如图2,![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 上的动点,
上的动点,![]() ,求四边形
,求四边形![]() 周长的最小值.
周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
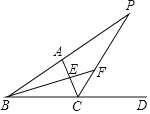
【题目】如图,已知BE是△ABC的角平分线,CP是△ABC的外角∠ACD的平分线.延长BE,BA分别交CP于点F,P.
(1)求证:∠BFC![]() ∠BAC;
∠BAC;
(2)小智同学探究后提出等式:∠BAC=∠ABC+∠P.请通过推理演算判断“小智发现”是否正确?
(3)若2∠BEC﹣∠P=180°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的任意两点M(x1,y1),N(x2,y2),给出如下定义:
将|x1﹣x2|称为点M,N之间的“横长”,|y1﹣y2|称为点M,N之间的纵长”,点M与点N的“横长”与“纵长”之和称为“折线距离”,记作d(M,N)=|x1﹣x2|+|y1﹣y2|“.
例如:若点M(﹣1,1),点N(2,﹣2),则点M与点N的“折线距离”为:d(M,N)=|﹣1﹣2|+|1﹣(﹣2)|=3+3=6.
根据以上定义,解决下列问题:
已知点P(3,2).
(1)若点A(a,2),且d(P,A)=5,求a的值;
(2)已知点B(b,b),且d(P,B)<3,直接写出b的取值范围;
(3)若第一象限内的点T与点P的“横长”与“纵长”相等,且d(P,T)>5,简要分析点T的横坐标t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知正比例函数![]() 与一次函数
与一次函数![]() 的图像交于点A.
的图像交于点A.
(1)求点A的坐标;
(2)设x轴上一点P(a,b),过点P作x轴的垂线(垂线位于点A的右侧),分别交![]() 和
和![]() 的图像于点B、C,连接OC,若BC=
的图像于点B、C,连接OC,若BC=![]() OA,求△OBC的面积.
OA,求△OBC的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com