
分析 (1)根据抛物线解析式可以得到对称轴x的值,根据开口向上,在对称轴右侧y随着x的增大而增大可以解答本题.
(2)根据抛物线的解析式可以求得点O、A、B的坐标,从而可以求得△OAB的面积.
解答 解:(1)∵抛物线y=3(x-2)2+4,
∴对称轴为x=2,开口向上.
∴x>2时,y随着x的增大而增大.
(2)∵抛物线y=3(x-2)2+4的顶点为A,原点为O,该抛物线交y轴于点B.
∴点A的坐标为(2,4),点O的坐标为(0,0),点B的坐标为(0,16).
∴${S}_{△OAB}=\frac{(16-0)×2}{2}=16$.
即△OAB的面积为16.
点评 本题考查二次函数的性质,解题的关键是明确二次函数的性质,a>0开口向上,a<0开口向下,以及在对称轴两侧y随x的增大的变化趋势.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:填空题
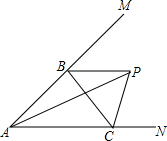 如图,点P在∠MAN内,点B,C分别是AM,AN上的点,∠MBC和∠NCB的平分线相交于点P.若∠APB=24°,则∠ACB的度数为48°.
如图,点P在∠MAN内,点B,C分别是AM,AN上的点,∠MBC和∠NCB的平分线相交于点P.若∠APB=24°,则∠ACB的度数为48°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 9 | C. | 7 | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | -1 | -2 | 3 | 1 | 1 | 2 | -$\frac{1}{2}$ |
| y | 3 | $\frac{3}{2}$ | -1 | -3 | -3 | -$\frac{3}{2}$ | 6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com