
| A. | 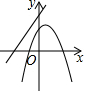 | B. | 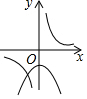 | C. | 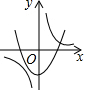 | D. | 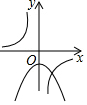 |
分析 先根据二次函数的开口方向确定二次项系数a的符号,看它是否满足反比例函数的图象,及二次函数与y轴的交点的位置.
解答 解:A、二次函数开口向下,则a<0,与y轴交于正半轴,所以a>0,所以选项A不正确;
B、二次函数开口向下,则a<0,所以y=$\frac{a}{x}$(a≠0)在一、三象限,所以选项B不正确;
C、二次函数开口向上,则a>0,与y轴交于负半轴,所以a<0,所以选项C不正确;
D、二次函数开口向下,则a<0,且交于y轴负半轴,所以y=$\frac{a}{x}$(a≠0)在二、四象限,所以选项D正确;
故选D.
点评 本题考查了二次函数的图象与性质及反比例函数的图象与性质,明确二次函数的开口方向确定a的正负:①开口向下→a<0,②开口向上→a>0,熟记二次函数与y轴的交点确定常数项c的值:①交于y轴正半轴→c>0,②交于y轴负半轴→c<0,③交于原点→c=0;反比例函数中,当k>0,双曲线的两支分别位于第一、第三象限,当k<0,双曲线的两支分别位于第二、第四象限.


科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,抛物线y=ax2+1经过点A(4,-3),顶点为点B,点P为抛物线上的一个动点,l是过点(0,2)且垂直于y轴的直线,过P作PH⊥l,垂足为H,连接PO.
如图,在平面直角坐标系xOy中,抛物线y=ax2+1经过点A(4,-3),顶点为点B,点P为抛物线上的一个动点,l是过点(0,2)且垂直于y轴的直线,过P作PH⊥l,垂足为H,连接PO.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
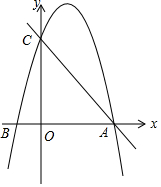 已知抛物线y=-x2+mx+m+1与x轴交于A、B两点(A在B点的右侧),与y轴交于点C.
已知抛物线y=-x2+mx+m+1与x轴交于A、B两点(A在B点的右侧),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a+b | B. | abc | C. | 1000a+10b+c | D. | 100c+10b+a |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0是最小的有理数 | |
| B. | 最大的负有理数是-1 | |
| C. | 任何有理数的绝对值都是正数 | |
| D. | 如果两个数互为相反数,那么它们的绝对值相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
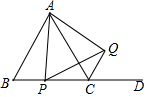 如图,△ABC是等边三角形,AB=2,动点P从点B出发,以1cm/s速度沿射线BC运动,连接AP,以AP为边向其右侧作等边三角形APQ,连按CQ,设点P的运动时间为t(s).
如图,△ABC是等边三角形,AB=2,动点P从点B出发,以1cm/s速度沿射线BC运动,连接AP,以AP为边向其右侧作等边三角形APQ,连按CQ,设点P的运动时间为t(s).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com