
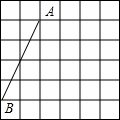
 如图,点A、B为6×6的网格中的格点,每个小正方形的边长都为1,其中A点的坐标为(0,4).
如图,点A、B为6×6的网格中的格点,每个小正方形的边长都为1,其中A点的坐标为(0,4).分析 (1)由A点的坐标为(0,4)可建立平面直角坐标系,由此即可求出点B的坐标;
(2)由(1)中的平面直角坐标系,当∠ACB=90°,利用勾股定理的逆定理即可求出符合条件的点C的坐标.
解答 解:(1)建立如图所示的平面直角坐标系,则点B(-2,0);
(2)如图所示: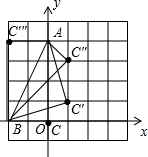 则C(0,0)或(-2,4)或C(1,1)或C(1,3).
则C(0,0)或(-2,4)或C(1,1)或C(1,3).
点评 本题考查了勾股定理以及其逆定理的运用,解题的关键是熟记勾股定理以及其逆定理.勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方;勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 240元 | B. | 280元 | C. | 320元 | D. | 360元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
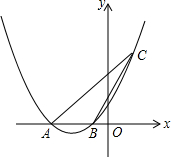 如图,二次函数y=$\frac{1}{4}$x2+($\frac{m}{4}$+1)x+m(其中m<4)的图象与x轴相交于A、B两点,且点A在点B的左侧.
如图,二次函数y=$\frac{1}{4}$x2+($\frac{m}{4}$+1)x+m(其中m<4)的图象与x轴相交于A、B两点,且点A在点B的左侧.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.5千米 | B. | 35千米 | C. | 350千米 | D. | 3500千米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com