【题目】如图，在四边形ABCD中，AD∥BC, AB=AC，BE=CE=AD.
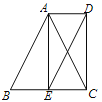
（1）求证：四边形ECDA是矩形；
（2）当△ABC是什么类型的三角形时，四边形ECDA是正方形？请说明理由.
【答案】(1)、证明过程见解析；(2)、当△ABC是等腰直角三角形时；证明过程见解析.
【解析】
试题分析：(1)、根据AD//EC且AD=EC得到平行四边形，然后根据AB=AC，BE=CE得出∠AEC=90°，则得到矩形；(2)、根据等腰直角三角形的性质得出AE=EC，从而得到正方形.
试题解析：(1)、在四边形AECD中,AD//EC且AD=EC. ∴ 四边形AECD是平行四边形
∵AB=AC，BE=CE ∴AE⊥BC ,∠AEC=90° ∴四边形AECD是矩形
、当△ABC是等腰直角三角形时，四边形ECDA是正方形
∵△ABC等腰直角三角形时，∠AEC=Rt∠,又因BE=CE ∴AE =
=CE
又∵四边形AECD是矩形 ∴四边形ECDA是正方形
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】以下是某校九年级10名同学参加学校演讲比赛的统计表．则这组数据的众数和中位数分别为（ ）．
成绩/分 | 80 | 85 | 90 | 95 |
人数/人 | 1 | 3 | 4 | 2 |
A.85，87.5B.85，85C.85，90D.90，90
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】把抛物线y=-x2向左平移1个单位，然后向上平移3个单位，则平移后抛物线的表达式为( )
A. y＝-x2+2x+2 B. y＝-x2-2x+2 C. y＝-x2+2x-4 D. y＝-x2-2x-4
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校课外兴趣小组在本校学生中开展对“消防安全知识”了解情况的专题调查活动，采取随机抽样的方式进行问卷调查，调查的结果分为A，B，C，D四类．其中，A类表示“非常了解”，B类表示“比较了解”，C类表示“基本了解”，D类表示“不太了解”，划分类别后的数据整理如下表格：
（1）根据表中数据，问在关于调查结果的扇形统计图中，类别为B的学生数所对应的扇形圆心角的度数为多少？
（2）若A类学生数比D类学生数的2倍少4,求表中a,m的值；
（3）若该校有学生955名，根据调查结果，估计该校学生中类别为C的人数约为多少？
查看答案和解析>>
科目：初中数学 来源： 题型：
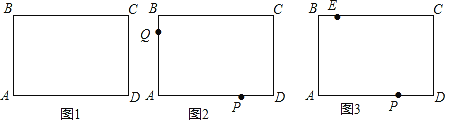
【题目】如图1，长方形ABCD中，∠A=∠B=∠C=∠D=90°，AB=CD，AD=BC，且
+|BC﹣6|=0，点P、Q分别是边AD、AB上的动点．
（1）求BD的长（长度单位是cm）；
（2）如图2，若点P从D点出发，以2cm/s的速度沿DA向点A运动，点Q从B点出发，以1cm/s的速度沿BA向点A运动，P、Q同时出发，一个点到达终点时，两点同时停止运动；设运动时间为x，用含x的代数式表示△CPQ的面积S．
（3）如图3，在BC上取一点E，使EB=1，那么当△EPC是等腰三角形时，请直接写出△EPC的周长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我区积极开展“体育大课间”活动，引导学生坚持体育锻炼．某校根据实际情况，决定主要开设A：乒乓球，B：篮球，C：跑步，D：足球四种运动项目．为了解学生最喜欢哪一种项目，随机抽取了部分学生进行调查，并将调查结果绘制成如下统计图．请你结合图中信息解答下列问题：
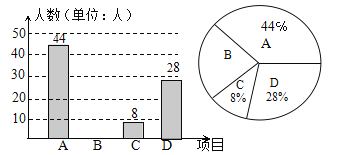
(1)求样本中最喜欢B项目的人数百分比和其所在扇形图中的圆心角的度数；
(2)请把条形统计图补充完整；
(3)已知该校有1000人，请根据样本估计全校最喜欢足球的人数是多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com