
【题目】如图所示,直线AB、CD相交于点O,OM⊥AB. 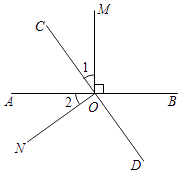
(1)若∠1=∠2,判断ON与CD的位置关系,并说明理由;
(2)若∠1= ![]() ∠BOC,求∠MOD的度数.
∠BOC,求∠MOD的度数.
【答案】
(1)解:ON⊥CD.
理由如下:
∵OM⊥AB,
∴∠AOM=90°,
∴∠1+∠AOC=90°,
又∵∠1=∠2,
∴∠2+∠AOC=90°,
即∠CON=90°,
∴ON⊥CD
(2)解:∵OM⊥AB, ![]() ∠BOC,
∠BOC,
∴∠1=30°,∠BOC=120°,
又∵∠1+∠MOD=180°,
∴∠MOD=180°﹣∠1=150°
【解析】(1)根据垂直定义可得∠AOM=90°,进而可得∠1+∠AOC=90°,再利用等量代换可得到∠2+∠AOC=90°,从而可得ON⊥CD;(2)根据垂直定义和条件可得∠1=30°,∠BOC=120°,再根据邻补角定义可得∠MOD的度数.
【考点精析】利用对顶角和邻补角和垂线的性质对题目进行判断即可得到答案,需要熟知两直线相交形成的四个角中,每一个角的邻补角有两个,而对顶角只有一个;垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)26﹣17+(﹣6)﹣33
(2)﹣14﹣ ![]() ×[3﹣(﹣3)2]
×[3﹣(﹣3)2]
(3)先化简,再求值:2ab2﹣3a2b﹣2(a2b+ab2),其中a=1,b=﹣2.
查看答案和解析>>
科目:初中数学 来源: 题型:
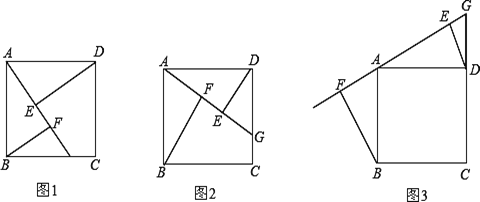
【题目】四边形ABCD是正方形(提示:正方形四边相等,四个角都是90°)
如图1,点G是BC边上任意一点(不与点B、C重合),连接AG,作BF⊥AG于点F,
DE⊥AG于点E.求证:△ABF≌△DAE;
(2) ①如图2,若点G是CD边上任意一点(不与点C、D重合),连接AG,作BF⊥AG于点F,
DE⊥AG于点E,线段EF与AF、BF的等量关系是______ ___;
②如图3,若点G是CD延长线上任意一点,连接AG,作BF⊥AG于点F,DE⊥AG于点E,
线段EF与AF、BF的等量关系是______ ;
(3)若点G是BC延长线上任意一点,连接AG,作BF⊥AG于点F,DE⊥AG于点E,请画图并
探究线段EF与AF、BF的等量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,老师和同学们判断一个四边形门框是否为矩形,下面是某合作学习小组的4位同学拟定的方案,其中正确的是( ).
A. 测量对角线是否相互平分 B. 测量两组对边是否分别相等
C. 测量一组对角是否都为直角 D. 测量其中三角形是否都为直角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中不能判定三角形全等的是( )
A. 两角和其中一角的对边对应相等 B. 三条边对应相等
C. 两边和它们的夹角对应相等 D. 三个角对应相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com