
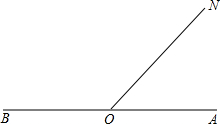
 如图,已知∠AOB=180°,射线ON.
如图,已知∠AOB=180°,射线ON. 还多47°,那么∠AON=______度.
还多47°,那么∠AON=______度.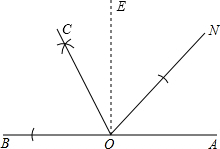 (1)如图所示,OC即为∠BON的平分线;
(1)如图所示,OC即为∠BON的平分线; (180°-50°)=65°,
(180°-50°)=65°, (180°-60°)=60°,
(180°-60°)=60°, ∠AON+47°+∠AON=180°,
∠AON+47°+∠AON=180°, 长度为半径画弧,两弧相交于一点,然后过点O与这点作射线OC即为所求;
长度为半径画弧,两弧相交于一点,然后过点O与这点作射线OC即为所求;

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:


查看答案和解析>>
科目:初中数学 来源: 题型:
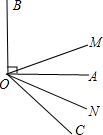
| A、45° | ||
B、45°+
| ||
C、60°-
| ||
| D、不能计算 |
查看答案和解析>>
科目:初中数学 来源: 题型:
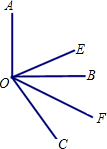 如图,已知∠AOB是直角,∠BOC=60°,OE平分∠AOC,OF平分∠BOC.
如图,已知∠AOB是直角,∠BOC=60°,OE平分∠AOC,OF平分∠BOC.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知∠AOB=x(0°<x<180°),OC平分∠AOB,点N为OB上一个定点.通过画图可以知道:当∠AOB=45°时,在射线OC上存在点P,使△ONP成为等腰三角形,且符合条件的点有三个,即P1(顶点为P2),P2(顶点为0),P3(顶点为N).
如图,已知∠AOB=x(0°<x<180°),OC平分∠AOB,点N为OB上一个定点.通过画图可以知道:当∠AOB=45°时,在射线OC上存在点P,使△ONP成为等腰三角形,且符合条件的点有三个,即P1(顶点为P2),P2(顶点为0),P3(顶点为N).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com