
等腰三角形一腰上的高与另一腰的夹角为360,则该等腰三角形的底角的度数为 .
63°或27°.
【解析】
试题分析:等腰三角形分锐角和钝角两种情况,求出每种情况的顶角的度数,再利用等边对等角的性质(两底角相等)和三角形的内角和定理,即可求出底角的度数:
有两种情况;
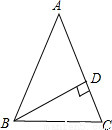
(1)如图当△ABC是锐角三角形时,BD⊥AC于D,则∠ADB=90°,
∵∠ABD=36°,∴∠A=90°-36°=54°.
∵AB=AC,∴∠ABC=∠C=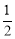 ×(180°-54°)=63°.
×(180°-54°)=63°.
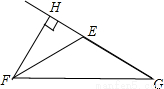
(2)如图 当△EFG是钝角三角形时,FH⊥EG于H,则∠FHE=90°,
∵∠HFE=36°,∴∠HEF=90°-36°=54°,∴∠FEG=180°-54°=126°.
∵EF=EG,∴∠EFG=∠G=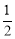 ×(180°-126°),=27°.
×(180°-126°),=27°.
考点:1.等腰三角形的性质;2.三角形内角和定理;分类思想的应用.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源:2014年初中毕业升学考试(四川内江卷)数学(解析版) 题型:选择题
按如图所示的程序计算,若开始输入的n值为 ,则最后输出的结果是( )
,则最后输出的结果是( )
A.14 B.16 C.8+5 D.14+
D.14+
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(北京卷)数学(解析版) 题型:解答题
已知关于 的方程
的方程 .
.
(1)求证:方程总有两个实数根;
(2)若方程的两个实数根都是整数,求正整数 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(内蒙古呼和浩特卷)数学(解析版) 题型:解答题
如图,已知直线l的解析式为 ,抛物线y = ax2+bx+2经过点A(m,0),B(2,0),D
,抛物线y = ax2+bx+2经过点A(m,0),B(2,0),D  三点.
三点.
(1)求抛物线的解析式及A点的坐标,并在图示坐标系中画出抛物线的大致图象;
(2)已知点 P(x,y)为抛物线在第二象限部分上的一个动点,过点P作PE垂直x轴于点E, 延长PE与直线l交于点F,请你将四边形PAFB的面积S表示为点P的横坐标x的函数, 并求出S的最大值及S最大时点P的坐标;
(3)将(2)中S最大时的点P与点B相连,求证:直线l上的任意一点关于x轴的对称点一定在PB所在直线上.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(内蒙古呼和浩特卷)数学(解析版) 题型:解答题
如图,一艘海轮位于灯塔P的北偏东65 方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45
方向,距离灯塔80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45 方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数及根式表示即可)
方向上的B处,这时,海轮所在的B处距离灯塔P有多远?(结果用非特殊角的三角函数及根式表示即可)

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(内蒙古包头、乌兰察布卷)数学(解析版) 题型:选择题
如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,EF∥AB.若AD=2BD,则 的值为( )
的值为( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市西城区中考一模数学试卷(解析版) 题型:解答题
平面直角坐标系 中,一次函数
中,一次函数 和反比例函数
和反比例函数 的图象都经过点
的图象都经过点 .
.
(1)求 的值和一次函数的表达式;
的值和一次函数的表达式;
(2)点B在双曲线 上,且位于直线
上,且位于直线 的下方,若点B的横、纵坐标都是整数,直接写出点B的坐标.
的下方,若点B的横、纵坐标都是整数,直接写出点B的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com