
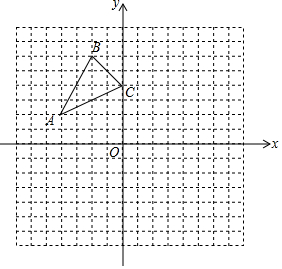
 如图,已知A (-4,2),B (-2,6),C (0,4)是直角坐标系平面上三点.
如图,已知A (-4,2),B (-2,6),C (0,4)是直角坐标系平面上三点.分析 (1)根据向右平移4个单位再向下平移1个单位得到△A1B1C1,画出平移后的图形即可;
(2)根据向右平移4个单位再向下平移1个单位,可知横坐标增加4,纵坐标减小1;
(3)根据以原点O为位似中心,将△ABC缩小为原来的一半,得到△A2B2C2即可.
解答 解:(1)如图所示,△A1B1C1即为所求;
(2)∵△ABC向右平移4个单位再向下平移1个单位,得到△A1B1C1,
∴点P (a,b)的对应点Pl的坐标为(a+4,b-1),
故答案为:(a+4,b-1);
(3)如图所示,△A2B2C2即为所求.
点评 本题主要考查了位似变换以及平移变换,解题时注意:①画一个图形的位似图形时,位似中心的选择是任意的,这个点可以在图形的内部或外部或在图形上,对于具体问题要考虑画图方便且符合要求.②由于位似中心选择的任意性,因此作已知图形的位似图形的结果是不唯一的.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:填空题
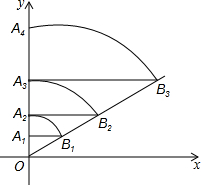 如图,直线l:y=$\frac{\sqrt{3}}{3}$x,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交y轴于点A2,再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,照此做法进行下去,点A2017的坐标为(0,22016).
如图,直线l:y=$\frac{\sqrt{3}}{3}$x,点A1坐标为(0,1),过点A1作y轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交y轴于点A2,再过点A2作y轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交y轴于点A3,…,照此做法进行下去,点A2017的坐标为(0,22016).查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 年龄组 | 12岁 | 13岁 | 14岁 | 15岁 |
| 参赛人数 | 5 | 19 | 13 | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 11 | 10 | 6 | 15 | 9 | 16 | 13 | 12 | 0 | 8 | 2 | 8 | 10 | 17 | 6 |
| 13 | 7 | 5 | 7 | 3 | 12 | 10 | 7 | 11 | 3 | 6 | 8 | 14 | 15 | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com