
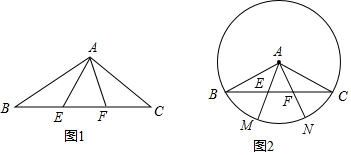
分析 (1)①只要证明△ABE≌△ACF即可解决问题.
②只要证明△AFE∽△BFA,可得$\frac{AF}{BF}$=$\frac{EF}{AF}$,设BE=AE=AF=CF=x,EF=y,即$\frac{x}{x+y}$=$\frac{y}{x}$,即x2-xy-y2=0,即($\frac{x}{y}$)2-($\frac{x}{y}$)-1=0,推出$\frac{x}{y}$=$\frac{1+\sqrt{5}}{2}$,由此即可解决问题.
(2)由题意△ABC为2型等腰三角形,可知BE=CF=2EF,设EF=a,则BE=CF=2a,由∠BAM=∠MAN=∠NAC,推出$\widehat{BM}$=$\widehat{NM}$=$\widehat{CN}$,推出∠BCM=∠CMN,∠MBC=∠MAN,BM=MN=CN,推出BC∥MN,由∠MBE=∠EAF,∠BEM=∠AEF,推出∠BME=∠AFE,由∠AEF=∠AFE,推出∠BME=∠BEM,推出BE=BM=MN=2a,由EF∥MN,推出$\frac{AE}{AM}$=$\frac{EF}{MN}$=$\frac{1}{2}$,推出AE=EM,设AE=EM=k,由△BEM∽△AEF,可得$\frac{BE}{AE}$=$\frac{EM}{EF}$,即$\frac{2a}{k}$=$\frac{k}{a}$,推出k=$\sqrt{2}$a,推出AB=AM=2k=2$\sqrt{2}$a,BC=5a,由此即可解决问题.
(3)求出等腰直角三角形是n型等腰三角形时的n的值即可解决问题.
解答 (1)①证明:如图1中,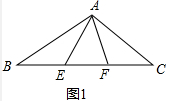
∵AB=AC,
∴∠B=∠C,
∵∠BAE=∠EAF=∠FAC,
在△ABE和△ACF中,
$\left\{\begin{array}{l}{∠B=∠C}\\{AB=AC}\\{∠BAE=∠CAF}\end{array}\right.$,
∴△ABE≌△ACF,
∴BE=CF.
②解:由①可知BE=CF,AE=AF,
∵BE=AE,
∴AF=CF,
∴∠B=∠BAE,设∠B=x则∠AEF=∠AFE=2x,
在△AEF中,∵∠EAF+∠AEF+∠AFE=180°,
∴5x=180°,
∴x=36°,
∴∠FAE=∠B=36°,∵∠AFE=∠AFB,
∴△AFE∽△BFA,
∴$\frac{AF}{BF}$=$\frac{EF}{AF}$,设BE=AE=AF=CF=x,EF=y,
∴$\frac{x}{x+y}$=$\frac{y}{x}$,
∴x2-xy-y2=0,
∴($\frac{x}{y}$)2-($\frac{x}{y}$)-1=0,
∴$\frac{x}{y}$=$\frac{1+\sqrt{5}}{2}$ 或$\frac{1-\sqrt{5}}{2}$(舍弃),
∴$\frac{BE}{EF}$=$\frac{1+\sqrt{5}}{2}$,
∴n=$\frac{1+\sqrt{5}}{2}$.
(2)如图2中,连接BM、MN、CN、CM.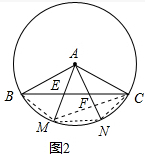
∵△ABC为2型等腰三角形,
∴BE=CF=2EF,设EF=a,则BE=CF=2a,
∵∠BAM=∠MAN=∠NAC,
∴$\widehat{BM}$=$\widehat{NM}$=$\widehat{CN}$,
∴∠BCM=∠CMN,∠MBC=∠MAN,BM=MN=CN,
∴BC∥MN,
∵∠MBE=∠EAF,∠BEM=∠AEF,
∴∠BME=∠AFE,∵∠AEF=∠AFE,
∴∠BME=∠BEM,
∴BE=BM=MN=2a,
∵EF∥MN,
∴$\frac{AE}{AM}$=$\frac{EF}{MN}$=$\frac{1}{2}$,
∴AE=EM,设AE=EM=k,
∵△BEM∽△AEF,
∴$\frac{BE}{AE}$=$\frac{EM}{EF}$,
∴$\frac{2a}{k}$=$\frac{k}{a}$,
∴k=$\sqrt{2}$a,
∴AB=AM=2k=2$\sqrt{2}$a,BC=5a,
∴$\frac{AB}{BC}$=$\frac{2\sqrt{2}}{5}$.
(3)如图3中,当∠BAC=90°时,作EM⊥AB于M,EN⊥AF于N.设BE=a.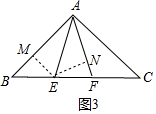
∵AB=AC,
∴∠B=∠C=45°,
∴BM=EM=$\frac{\sqrt{2}}{2}$a,
∵∠BAE=∠EAF=∠CAF=30°,
在Rt△AME中,AE=2EM=$\sqrt{2}$a,
∵∠EAM=∠EAN,EM⊥AB,EN⊥AF,
∴EM=EN=$\frac{\sqrt{2}}{2}$a,
在Rt△AEN中,AN=$\sqrt{3}$NE=$\frac{\sqrt{6}}{2}$a,
∵AE=AF=$\sqrt{2}$a,
∴FN=$\sqrt{2}$a-$\frac{\sqrt{6}}{2}$a,
∴EF=$\sqrt{E{N}^{2}+F{N}^{2}}$=$\sqrt{(\frac{\sqrt{2}}{2}a)^{2}+(\sqrt{2}a-\frac{\sqrt{6}}{2}a)^{2}}$=($\sqrt{3}$-1)a,
∴$\frac{BE}{EF}$=$\frac{a}{(\sqrt{3}-1)a}$=$\frac{\sqrt{3}+1}{2}$,
∴n=$\frac{\sqrt{3}+1}{2}$.
由(1)可知,随∠BAC的减小,n的值在减小,且BE>EF,
∴n型等腰三角形,若顶角为锐角,n的取值范是1<n<$\frac{\sqrt{3}+1}{2}$.
点评 本题考查圆综合题、等腰三角形的性质、相似三角形的判定和性质、勾股定理、平行线的性质等知识,解题的关键是理解题意,学会利用参数构建方程解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
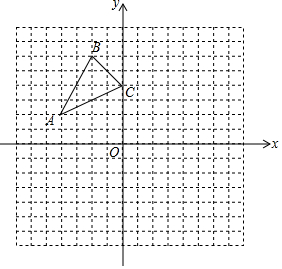 如图,已知A (-4,2),B (-2,6),C (0,4)是直角坐标系平面上三点.
如图,已知A (-4,2),B (-2,6),C (0,4)是直角坐标系平面上三点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
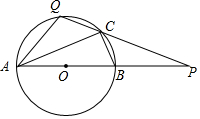 已知如图:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q是半圆上一动点(不与A、B重合),连接PQ,交⊙O于点C.下列结论:①∠QAP=∠BCP;②$\frac{CP}{QP}$=$\frac{BP}{AP}$;若点Q为劣弧$\widehat{AC}$的中点,则C是PQ的中点;④若点Q与C重合时,则PQ=2$\sqrt{3}$.其中正确的是①③④0(把所有正确结论的序号都选上)
已知如图:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q是半圆上一动点(不与A、B重合),连接PQ,交⊙O于点C.下列结论:①∠QAP=∠BCP;②$\frac{CP}{QP}$=$\frac{BP}{AP}$;若点Q为劣弧$\widehat{AC}$的中点,则C是PQ的中点;④若点Q与C重合时,则PQ=2$\sqrt{3}$.其中正确的是①③④0(把所有正确结论的序号都选上)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com