
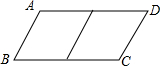
 邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作,在余下的四边形纸片中再剪去一个菱形,余下一个四边形,称为第二次操作,…依此类推,若第n次余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图,?ABCD中,若AB=1,BC=2,则□ABCD为1阶准菱形.
邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作,在余下的四边形纸片中再剪去一个菱形,余下一个四边形,称为第二次操作,…依此类推,若第n次余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图,?ABCD中,若AB=1,BC=2,则□ABCD为1阶准菱形.分析 (1)根据邻边长分别为2和3的平行四边形经过两次操作,即可得出所剩四边形是菱形,即可得出答案;
(2)利用3阶准菱形的定义,即可得出答案.
解答 解:(1)利用邻边长分别为2和3的平行四边形经过两次操作,所剩四边形是边长为1的菱形,
故邻边长分别为2和3的平行四边形是2阶准菱形;
故答案为:2;
(2)如图,必为a>3,且a=4;
②如图,必为2<a<3,且a=2.5;
③如图,必为$\frac{3}{2}$<a<2,且a-1+$\frac{1}{2}$(a-1)=1,解得a=$\frac{5}{3}$;
④如图,必为1<a<1.5,且3(a-1)=1,解得a=$\frac{4}{3}$.
综上所述,a的值分别是:a1=4,a2=2.5,a3=$\frac{5}{3}$,a4=$\frac{4}{3}$.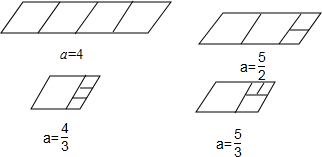
点评 此题主要考查了图形的剪拼以及菱形的判定,根据已知n阶准菱形定义正确将平行四边形分割是解题关键.


科目:初中数学 来源: 题型:解答题
 已知:一次函数y=2x+4
已知:一次函数y=2x+4查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
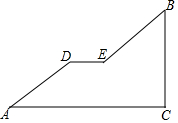 如图是一座人行天桥引桥部分的示意图,上桥通道由两段互相平行并且与地面成37°角楼梯AD,BE和一段水平平台DE构成.已知天桥的高度BC为4.8米,引桥的水平跨度AC为8米,求水平平台DE的长度.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图是一座人行天桥引桥部分的示意图,上桥通道由两段互相平行并且与地面成37°角楼梯AD,BE和一段水平平台DE构成.已知天桥的高度BC为4.8米,引桥的水平跨度AC为8米,求水平平台DE的长度.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com