
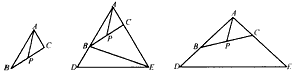
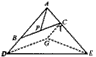
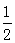 (AB+AC);
(AB+AC);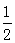 DE。
DE。| 解:(1)证明:延长AP至H,使得PH=AP,连接BH、HC ∵BP=PC ∴四边形ABHC是平行四边形, ∴AB=HC 在△ACH中,AH<HC+AC ∴2AP<AB+AC,即AP< 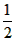 (AB+AC); (AB+AC); |
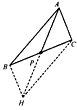 |
| (2)①解:BE=2AP 证明:过B作BH∥AE交DE于H,连接CH、AH ∴∠1=∠BAC=60° ∵DB=AC,AB=CE, ∴AD=AE ∴△AED是等边三角形, ∴∠D=∠1=∠2=60° ∴△BDH是等边三角形 ∴BD=DH=BH=AC ∴四边形ABHC是平行四边形 ∵点P是BC的中点, ∴AH、BC互相平分于点P,即AH=2AP, 在△ADH和△EDB中 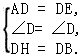 ∴△ADH≌△EDB ∴AH=BE=2AP; |
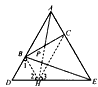 |
| ②证明:分两种情况: i.当AB=AC时, ∴AB=AC=DB=CE ∴BC= 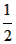 DE; DE; |
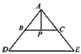 |
| II.当AB≠AC时,以BD、BC为一组邻边作平行四边形BDGC(如图), ∴DB=GC=AC,∠BAC=∠1,BC=DC ∵AB=CE ∴△ABC≌△CEC ∴BC=EC=DG 在△DGE中,DG+GE>DE ∴2BC>DE,即BC> 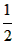 DE,综上所述,BC≥ DE,综上所述,BC≥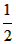 DE。 DE。 |
 |


科目:初中数学 来源: 题型:
 如图,在△ABC中,点D为边BC的中点,过点A作射线AE,过点C作CF⊥AE于点F,过点B作BG⊥AE于点G,连接FD并延长,交BG于点H
如图,在△ABC中,点D为边BC的中点,过点A作射线AE,过点C作CF⊥AE于点F,过点B作BG⊥AE于点G,连接FD并延长,交BG于点H查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
 阅读:定理“直角三角形斜边上的中线等于斜边的一半”,如图,Rt△ABC中,D为AB中点,则CD=AD=BD=
阅读:定理“直角三角形斜边上的中线等于斜边的一半”,如图,Rt△ABC中,D为AB中点,则CD=AD=BD=| 1 | 2 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com