
(本题满分10分)
用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地面:

(1)观察图形,填写下表:
图形 | (1) | (2) | (3) | |
黑色瓷砖的块数 | 4 | 7 | ||
黑白两种瓷砖的总块数 | 15 | 25 |
(2)依上推测,第n个图形中黑色瓷砖的块数为 ;黑白两种瓷砖的总块数为 (都用含n的代数式表示)
(3)白色瓷砖的块数可能比黑色瓷砖的块数多2015块吗?若能,求出是第几个图形;若不能,请说明理由.
(1)10, 35 2分(2)3n+1, 10n+5 6分
(3) 8分
8分
解得:n=503
答:第503个图形. 10分
【解析】
试题分析:(1)第一个图形有黑色瓷砖3+1=4块,黑白两种瓷砖的总块数为3×5块;
第二个图形有黑色瓷砖3×2+1=7块,黑白两种瓷砖的总块数为5×5块;
第三个图形有黑色瓷砖3×3+1=10块,黑白两种瓷砖的总块数为7×5块;
(2)第n个图形中需要黑色瓷砖3n+1块,黑白两种瓷砖的总块数为(2n+1)×5块;
(3) 根据白色瓷砖的块数可能比黑色瓷砖的块数多2015块列出方程,解方程即可.
试题解析:(1)第一个图形有黑色瓷砖3+1=4块,黑白两种瓷砖的总块数为3×5=15块;
第二个图形有黑色瓷砖3×2+1=7块,黑白两种瓷砖的总块数为5×5=25块;
第三个图形有黑色瓷砖3×3+1=10块,黑白两种瓷砖的总块数为7×5=35块;
(2)第n个图形中需要黑色瓷砖3n+1块,黑白两种瓷砖的总块数为(2n+1)×5=10n+5块;
(3)根据题意可得: ,解得:n=503
,解得:n=503
答:第503个图形.
考点:1.探寻规律;2.列代数式及求值;3.一元一次方程的应用.


科目:初中数学 来源:2014-2015学年黑龙江省大庆市林甸县九年级上学期期末检测数学试卷(解析版) 题型:填空题
某企业2010年底缴税40万元,2012年底缴税48.4万元,设这两年该企业缴税的年平均增长率为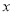 ,根据题意,可得方程_______________.
,根据题意,可得方程_______________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年陕西省七年级上期末测试数学试卷(解析版) 题型:选择题
某商场把一个双肩背书包按进价提高50%标价,然后再按八折出售,这样商场每卖出一个书包就可赢利8元.设每个双肩背书包的进价是x元,根据题意列一元一次方程,正确的是( ).
A.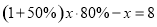 B.
B.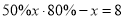
C.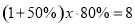 D.
D.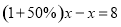
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB是池塘两端,设计一方法测量AB的距离,取点C,连接AC、BC,再取它们的中点D、E,测得DE=15米,则AB=( )
A.7.5米 B.15米 C.22.5米 D.30米
D.30米

查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省七年级上学期期末调研数学试卷(解析版) 题型:解答题
(本题满分6分)已知:如图,∠AOB=∠COD=90°

求:(1)∠AOC等于∠BOD吗?请说明理由;
(2)若∠BOD=136°,∠BOC等于多少度?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省七年级上学期期末调研数学试卷(解析版) 题型:填空题
如图是在正方形网格中按规律填成的阴影,根据此规律,则第n个图中阴影部分小正方形的个数是 .
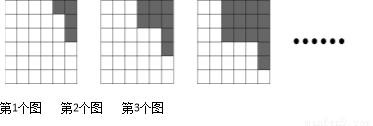
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省八年级上学期期末调研数学试卷(解析版) 题型:解答题
(本题满分12分)如图,直线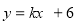 与x轴y轴分别相交于点E,F.点E的坐标(8,0),点A的坐标为(6,0)。点P(x,y)是第一象限内的直线上的一个动点(点P不与点E,F重合).
与x轴y轴分别相交于点E,F.点E的坐标(8,0),点A的坐标为(6,0)。点P(x,y)是第一象限内的直线上的一个动点(点P不与点E,F重合).
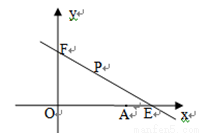
(1)求k的值;
(2)在点P运动的过程中,求出△OPA的面积S与x的函数关系式.
(3)若△OPA的面积为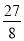 ,求此时点P的坐标.
,求此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏常州西藏民族中学七年级上学期期末联考数学试卷(解析版) 题型:填空题
已知小麦在磨成面粉后,质量要减少25%,为了得到600kg面粉,需要小麦 kg;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com