
ЁОЬтФПЁПаЁКьдкМЦЫу ЪБЃЌФУГі 1 еХЕШБпШ§НЧаЮжНЦЌАДШчЭМЫљЪОЗНЪННјааВйзїЃЎ
ЪБЃЌФУГі 1 еХЕШБпШ§НЧаЮжНЦЌАДШчЭМЫљЪОЗНЪННјааВйзїЃЎ
ЂйШчЭМ1ЃЌАб 1 ИіЕШБпШ§НЧаЮЕШЗжГЩ 4 ИіЭъШЋЯрЭЌЕФЕШБпШ§НЧаЮЃЌЭъГЩЕк 1 ДЮВйзїЃЛ
ЂкШчЭМ 2ЃЌдйАбЂйжазюЩЯУцЕФШ§НЧаЮЕШЗжГЩ 4 ИіЭъШЋЯрЭЌЕФЕШБпШ§НЧаЮЃЌЭъГЩЕк 2 ДЮВйзїЃЛ
ЂлШчЭМ 3ЃЌдйАбЂкжазюЩЯУцЕФШ§НЧаЮЕШЗжГЩ 4 ИіЭъШЋЯрЭЌЕФЕШБпШ§НЧаЮЃЌЁЄЁЄЁЄЁЄЁЄЁЄвРДЮжиИДЩЯЪіВйзїЃЎПЩЕУ ЕФжЕзюНгНќЕФЪ§ЪЧЃЈ ЃЉ
ЕФжЕзюНгНќЕФЪ§ЪЧЃЈ ЃЉ

A.![]() B.
B.![]() C.
C.![]() D.1
D.1
ЁОД№АИЁПA
ЁОНтЮіЁП
ЩшДѓШ§НЧаЮЕФУцЛ§ЮЊ1ЃЌЯШЧѓдЫуЪН3БЖЕФжЕЃЌНЋЦфжЕзЊЛЏЮЊШ§НЧаЮЕФУцЛ§КЭЃЌРћгУУцЛ§ЧѓНт.
НтЃКЩшДѓШ§НЧаЮЕФУцЛ§ЮЊ1ЃЌдђЕквЛДЮВйзїКѓУПИіаЁШ§НЧаЮЕФУцЛ§ЮЊ![]() ЃЌЕкЖўДЮВйзїКѓУПИіаЁШ§НЧаЮЕФУцЛ§ЮЊ
ЃЌЕкЖўДЮВйзїКѓУПИіаЁШ§НЧаЮЕФУцЛ§ЮЊ![]() ЃЌЕкШ§ДЮВйзїКѓУПИіаЁШ§НЧаЮУцЛ§ЮЊ
ЃЌЕкШ§ДЮВйзїКѓУПИіаЁШ§НЧаЮУцЛ§ЮЊ![]() ЃЌЕкЫФДЮВйзїКѓУПИіаЁШ§НЧаЮУцЛ§ЮЊ
ЃЌЕкЫФДЮВйзїКѓУПИіаЁШ§НЧаЮУцЛ§ЮЊ![]() ЃЌЁЁЕк2020ДЮВйзїКѓУПИіаЁШ§НЧаЮУцЛ§ЮЊ
ЃЌЁЁЕк2020ДЮВйзїКѓУПИіаЁШ§НЧаЮУцЛ§ЮЊ ЃЌЫуЪН
ЃЌЫуЪН ЯрЕБгкЭМ1жаЕФвѕгАВПЗжУцЛ§КЭ.НЋетИіЫуЪНРЉДѓ3БЖЃЌЕУ
ЯрЕБгкЭМ1жаЕФвѕгАВПЗжУцЛ§КЭ.НЋетИіЫуЪНРЉДѓ3БЖЃЌЕУ ЃЌДЫЪБИУЫуЪНЯрЕБгкЭМ2жавѕгАВПЗжУцЛ§КЭЃЌетИіКЭЕШгкДѓШ§НЧаЮУцЛ§МѕШЅ1ИіЪЃгрПеАзаЁШ§НЧаЮУцЛ§ЃЌМД
ЃЌДЫЪБИУЫуЪНЯрЕБгкЭМ2жавѕгАВПЗжУцЛ§КЭЃЌетИіКЭЕШгкДѓШ§НЧаЮУцЛ§МѕШЅ1ИіЪЃгрПеАзаЁШ§НЧаЮУцЛ§ЃЌМД ЃЌдђдЫуЪНЕФжЕЮЊ
ЃЌдђдЫуЪНЕФжЕЮЊ .
.
Ыљвд ЕФжЕзюНгНќ
ЕФжЕзюНгНќ![]() .
.

ЙЪбЁЃКA.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
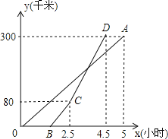
ЁОЬтФПЁПМзЁЂввСНЕиЯрОр300ЧЇУзЃЌвЛСОЛѕГЕКЭвЛСОНЮГЕЯШКѓДгМзЕиГіЗЂЯђввЕиЃЌШчЭМЃЌЯпЖЮOAБэЪОЛѕГЕРыМзЕиОрРыyЃЈЧЇУзЃЉгыЪБМфxЃЈаЁЪБЃЉжЎМфЕФКЏЪ§ЙиЯЕЃЛелЯпBCDБэЪОНЮГЕРыМзЕиОрРыyЃЈЧЇУзЃЉгыxЃЈаЁЪБЃЉжЎМфЕФКЏЪ§ЙиЯЕЃЎЕБНЮГЕЕНДяввЕиКѓЃЌТэЩЯбидТЗвдCDЖЮЫйЖШЗЕЛиЃЌдђЛѕГЕДгМзЕиГіЗЂ_______аЁЪБКѓгыНЮГЕЯргіЃЈНсЙћОЋШЗЕН0.01ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдк![]() жаЃЌBDЪЧЫќЕФвЛЬѕЖдНЧЯпЃЌЙ§AЁЂCСНЕуЗжБ№зї
жаЃЌBDЪЧЫќЕФвЛЬѕЖдНЧЯпЃЌЙ§AЁЂCСНЕуЗжБ№зї![]() ЃЌ
ЃЌ![]() ЃЌEЁЂFЮЊДЙзуЃЎ
ЃЌEЁЂFЮЊДЙзуЃЎ
ЃЈ1ЃЉШчЭМЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
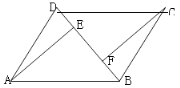
ЃЈ2ЃЉШчЭМЃЌСЌНгACЃЌЩшACЁЂBDНЛгкЕуOЃЌШє![]() ЃЎдкВЛЬэМгШЮКЮИЈжњЯпЕФЧщПіЯТЃЌЧыжБНгаДГіЭМжаЕФЫљгаГЄЖШЪЧOEГЄЖШ2БЖЕФЯпЖЮЃЎ
ЃЎдкВЛЬэМгШЮКЮИЈжњЯпЕФЧщПіЯТЃЌЧыжБНгаДГіЭМжаЕФЫљгаГЄЖШЪЧOEГЄЖШ2БЖЕФЯпЖЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЮФЛЏгУЦЗЩЬЕъгУ1 000дЊЙКНјвЛХњЁАГПЙтЁБЬзГпЃЌКмПьЯњЪлвЛПеЃЛЩЬЕъгжгУ1 500дЊЙКНјЕкЖўХњИУПюЬзГпЃЌЙКНјЪБЕЅМлЪЧЕквЛХњЕФ![]() БЖЃЌЫљЙКЪ§СПБШЕквЛХњЖр100ЬзЃЎ
БЖЃЌЫљЙКЪ§СПБШЕквЛХњЖр100ЬзЃЎ
ЃЈ1ЃЉЧѓЕквЛХњЬзГпЙКНјЪБЕЅМлЪЧЖрЩйЃП
ЃЈ2ЃЉШєЩЬЕъвдУПЬз4дЊЕФМлИёНЋетСНХњЬзГпШЋВПЪлГіЃЌПЩвдгЏРћЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП(1)ЛЏМђЧѓжЕЃК(2ЃЋa)(2Ѓa)ЃЋa(aЃ2b)ЃЋ3a5bЁТ(Ѓa2b)4ЃЌЦфжаabЃНЃ![]() .
.
(2)вђЪНЗжНтЃКa(nЃ1)2Ѓ2a(nЃ1)ЃЋa.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
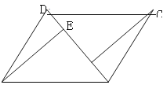
ЁОЬтФПЁПШчЭМЃЌЕуAЪЧЫЋЧњЯпy=![]() дкЕквЛЯѓЯоЩЯЕФвЛЖЏЕуЃЌСЌНгAOВЂбгГЄНЛСэвЛЗжжЇгкЕуBЃЌвдABЮЊаББпзїЕШбќRtЁїABCЃЌЕуCдкЕкЖўЯѓЯоЃЌЫцзХЕуAЕФдЫЖЏЃЌЕуCЕФЮЛжУвВВЛЖЯЕФБфЛЏЃЌЕЋЪМжедквЛКЏЪ§ЭМЯѓЩЯдЫЖЏЃЌдђетИіКЏЪ§ЕФНтЮіЪНЮЊ ЃЎ
дкЕквЛЯѓЯоЩЯЕФвЛЖЏЕуЃЌСЌНгAOВЂбгГЄНЛСэвЛЗжжЇгкЕуBЃЌвдABЮЊаББпзїЕШбќRtЁїABCЃЌЕуCдкЕкЖўЯѓЯоЃЌЫцзХЕуAЕФдЫЖЏЃЌЕуCЕФЮЛжУвВВЛЖЯЕФБфЛЏЃЌЕЋЪМжедквЛКЏЪ§ЭМЯѓЩЯдЫЖЏЃЌдђетИіКЏЪ§ЕФНтЮіЪНЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
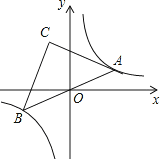
ЁОЬтФПЁПЁїABCдкЦНУцжБНЧзјБъЯЕxOyжаЕФЮЛжУШчЭМЫљЪОЃЎ
ЃЈ1ЃЉзїЁїABCЙигкЕуCГЩжааФЖдГЦЕФЁїA1B1C1ЃЛ
ЃЈ2ЃЉНЋЁїA1B1C1ЯђгвЦНвЦ3ИіЕЅЮЛЃЌзїГіЦНвЦКѓЕФЁїA2B2C2ЃЛ
ЃЈ3ЃЉдкxжсЩЯЧѓзївЛЕуPЃЌЪЙPA1+PC2ЕФжЕзюаЁЃЌВЂЧѓзюаЁжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯпy=ax2+bx+3ЃЈaЁй0ЃЉОЙ§ЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ![]() ЃЌ0ЃЉЃЌЧвгыyжсЯрНЛгкЕуCЃЎ
ЃЌ0ЃЉЃЌЧвгыyжсЯрНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓетЬѕХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉЧѓЁЯACBЕФЖШЪ§ЃЛ
ЃЈ3ЃЉЩшЕуDЪЧЫљЧѓХзЮяЯпЕквЛЯѓЯоЩЯвЛЕуЃЌЧвдкЖдГЦжсЕФгвВрЃЌЕуEдкЯпЖЮACЩЯЃЌЧвDEЁЭACЃЌЕБЁїDCEгыЁїAOCЯрЫЦЪБЃЌЧѓЕуDЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌвдACЮЊжБОЖзїЁбOЃЌНЛABгкDЃЌЙ§ЕуOзїOEЁЮABЃЌНЛBCгкEЃЎ
ЃЈ1ЃЉЧѓжЄЃКEDЮЊЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШчЙћЁбOЕФАыОЖЮЊ![]() ЃЌED=2ЃЌбгГЄEOНЛЁбOгкFЃЌСЌНгDFЁЂAFЃЌЧѓЁїADFЕФУцЛ§ЃЎ
ЃЌED=2ЃЌбгГЄEOНЛЁбOгкFЃЌСЌНгDFЁЂAFЃЌЧѓЁїADFЕФУцЛ§ЃЎ

ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉ![]()
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉЪзЯШСЌНгODЃЌгЩOEЁЮABЃЌИљОнЦНааЯпгыЕШбќШ§НЧаЮЕФаджЪЃЌвзжЄЕУ![]() Ёе
Ёе![]() МДПЩЕУ
МДПЩЕУ![]() ЃЌдђПЩжЄЕУ
ЃЌдђПЩжЄЕУ![]() ЮЊ
ЮЊ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
ЃЈ2ЃЉСЌНгCDЃЌИљОнжБОЖЫљЖдЕФдВжмНЧЪЧжБНЧЃЌМДПЩЕУ![]() РћгУЙДЙЩЖЈРэМДПЩЧѓЕУ
РћгУЙДЙЩЖЈРэМДПЩЧѓЕУ![]() ЕФГЄЃЌгжгЩOEЁЮABЃЌжЄЕУ
ЕФГЄЃЌгжгЩOEЁЮABЃЌжЄЕУ![]() ИљОнЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЃЌМДПЩЧѓЕУ
ИљОнЯрЫЦШ§НЧаЮЕФЖдгІБпГЩБШР§ЃЌМДПЩЧѓЕУ![]() ЕФГЄЃЌШЛКѓРћгУШ§НЧКЏЪ§ЕФжЊЪЖЃЌЧѓЕУ
ЕФГЄЃЌШЛКѓРћгУШ§НЧКЏЪ§ЕФжЊЪЖЃЌЧѓЕУ![]() гы
гы![]() ЕФГЄЃЌШЛКѓРћгУSЁїADF=SЬнаЮABEF-SЬнаЮDBEFЧѓЕУД№АИЃЎ
ЕФГЄЃЌШЛКѓРћгУSЁїADF=SЬнаЮABEF-SЬнаЮDBEFЧѓЕУД№АИЃЎ
ЪдЬтНтЮіЃК(1)жЄУїЃКСЌНгODЃЌ

ЁпOEЁЮABЃЌ
ЁрЁЯCOE=ЁЯCADЃЌЁЯEOD=ЁЯODAЃЌ
ЁпOA=OD,
ЁрЁЯOAD=ЁЯODAЃЌ
ЁрЁЯCOE=ЁЯDOEЃЌ
дкЁїCOEКЭЁїDOEжаЃЌ
 ЁрЁїCOEЁеЁїDOE(SAS)ЃЌ
ЁрЁїCOEЁеЁїDOE(SAS)ЃЌ
![]()
ЁрEDЁЭODЃЌ
ЁрEDЪЧ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
(2)СЌНгCDЃЌНЛOEгкMЃЌ
дкRtЁїODEжаЃЌ
ЁпOD=32ЃЌDE=2ЃЌ
![]()
ЁпOEЁЮABЃЌ
ЁрЁїCOEЁзЁїCABЃЌ
![]() ЁрAB=5ЃЌ
ЁрAB=5ЃЌ
ЁпACЪЧжБОЖЃЌ
![]()
![]()
![]()
![]()
ЁпEFЁЮABЃЌ
![]()
![]()
![]()
ЁрSЁїADF=SЬнаЮABEFSЬнаЮDBEF
![]()
ЁрЁїADFЕФУцЛ§ЮЊ![]()

ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
25
ЁОЬтФПЁПЁОЬтФПЁПвбжЊЃЌХзЮяЯпy=ax2+ax+bЃЈaЁй0ЃЉгыжБЯпy=2x+mгавЛИіЙЋЙВЕуMЃЈ1ЃЌ0ЃЉЃЌЧвaЃМbЃЎ
ЃЈ1ЃЉЧѓbгыaЕФЙиЯЕЪНКЭХзЮяЯпЕФЖЅЕуDзјБъЃЈгУaЕФДњЪ§ЪНБэЪОЃЉЃЛ
ЃЈ2ЃЉжБЯпгыХзЮяЯпЕФСэЭтвЛИіНЛЕуМЧЮЊNЃЌЧѓЁїDMNЕФУцЛ§гыaЕФЙиЯЕЪНЃЛ
ЃЈ3ЃЉa=Љ1ЪБЃЌжБЯпy=Љ2xгыХзЮяЯпдкЕкЖўЯѓЯоНЛгкЕуGЃЌЕуGЁЂHЙигкдЕуЖдГЦЃЌЯжНЋЯпЖЮGHбиyжсЯђЩЯЦНвЦtИіЕЅЮЛЃЈtЃО0ЃЉЃЌШєЯпЖЮGHгыХзЮяЯпгаСНИіВЛЭЌЕФЙЋЙВЕуЃЌЪдЧѓtЕФШЁжЕЗЖЮЇЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com