
科目:初中数学 来源: 题型:
阅读下列材料:
小明遇到一个问题:5个同样大小的正方形纸片排列形式如图1所示,将它们分割后拼接成一个新的正方形.他的做法是:按图2所示的方法分割后,将三角形纸片①绕AB的中点O旋转至三角形纸片②处,依此方法继续操作,即可拼接成一个新的正方形DEFG.
请你参考小明的做法解决下列问题:
⑴ 现有5个形状、大小相同的矩形纸片,排列形式如图3所示.请将其分割后拼接成一个平行四边形.在图3中画出示意图,标注字母,指明拼接而成的平行四边形;
⑵ 如图4,在面积为2的平行四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,分别连结AF、BG、CH、DE得到一个新的平行四边形MNPQ,请在图4中探究平行四边形MNPQ面积的大小(画图并直接写出结果).
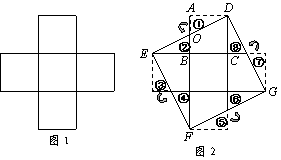
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
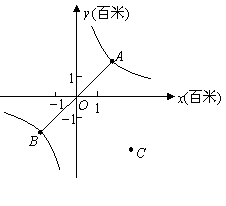
如图,帆船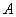 和帆船
和帆船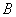 在太湖湖面上训练,
在太湖湖面上训练,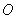 为湖面上的一个定点,教练船静候于
为湖面上的一个定点,教练船静候于 点.训练时要求
点.训练时要求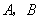 两船始终关于
两船始终关于 点对称.以
点对称.以 为原点,建立如图所示的坐标系,
为原点,建立如图所示的坐标系,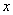 轴,
轴, 轴的正方向分别表示正东、正北方向.设
轴的正方向分别表示正东、正北方向.设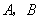 两船可近似看成在双曲线
两船可近似看成在双曲线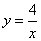 上运动.湖面风平浪静,双帆远影优美.训练中当教练船与
上运动.湖面风平浪静,双帆远影优美.训练中当教练船与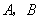 两船恰好在直线
两船恰好在直线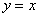 上时,三船同时发现湖面上有一遇险的
上时,三船同时发现湖面上有一遇险的 船,此时教练船测得
船,此时教练船测得 船在东南
船在东南 方向上,
方向上,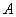 船测得
船测得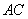 与
与 的夹角为
的夹角为 ,
,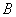 船也同时测得
船也同时测得 船的位置(假设
船的位置(假设 船位置不再改变,
船位置不再改变,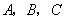 三船可分别用
三船可分别用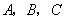 三点表示).
三点表示).
(1)发现 船时,
船时,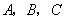 三船所在位置的坐标分别为
三船所在位置的坐标分别为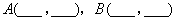 和
和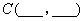 ;
;
(2)发现 船,三船立即停止训练,并分别从
船,三船立即停止训练,并分别从 三点出发船沿最短路线同时前往救援,设
三点出发船沿最短路线同时前往救援,设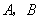 两船的速度相等,教练船与
两船的速度相等,教练船与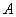 船的速度之比为
船的速度之比为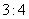 ,问教练船是否最先赶到?请说明理由.
,问教练船是否最先赶到?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com