练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    ⊙O的半径为2，弦BC=2，点A是⊙O上一点，且AB=AC，直线AO与BC交于点D，则AD的长为　 　．

     

    1或3

    【解析】

    试题分析：如图所示：

    ∵⊙O的半径为2，弦BC=2，点A是⊙O上一点，且AB=AC，

    ∴AD⊥BC，

    ∴BD=BC=，

    在Rt△OBD中，

    ∵BD2+OD2=OB2，即（）2+OD2=22，解得OD=1，

    ∴当如图1所示时，AD=OA﹣OD=2﹣1=1；

    当如图2所示时，AD=OA+OD=2+1=3．

    故答案为：1或3．

    考点：1、垂径定理；2、勾股定理．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2013-2014学年北京市顺义区中考一模数学试卷（解析版） 题型：选择题

    某市在一次扶贫助残活动中，共捐款3 580 000元，将3 580 000用科学记数法表示为（ ）

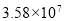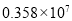    A．　　　 　B． C．　　　 D．

     

    查看答案和解析>>

    科目：初中数学 来源：2014年初中毕业升学考试（黑龙江绥化卷）数学（解析版） 题型：选择题

    如图是一个由多个相同小正方体搭成的几何体的俯视图，图中所标数字为该位置小正方体的个数，则这个几何体的左视图是（　　）

    A． B． C． D．

     

    查看答案和解析>>

    科目：初中数学 来源：2014年初中毕业升学考试（黑龙江牡丹江卷）数学（解析版） 题型：解答题

    如图，在等边△ABC中，点D在直线BC上，连接AD，作∠ADN=60°，直线DN交射线AB于点E，过点C作CF∥AB交直线DN于点F．

    （1）当点D在线段BC上，∠NDB为锐角时，如图①，求证：CF+BE=CD；

    （提示：过点F作FM∥BC交射线AB于点M．）

    （2）当点D在线段BC的延长线上，∠NDB为锐角时，如图②；当点D在线段CB的延长线上，∠NDB为钝角时，如图③，请分别写出线段CF，BE，CD之间的数量关系，不需要证明；

    （3）在（2）的条件下，若∠ADC=30°，S△ABC=4，则BE=　 　，CD=　 ．

     

    查看答案和解析>>

    科目：初中数学 来源：2014年初中毕业升学考试（黑龙江牡丹江卷）数学（解析版） 题型：填空题

    如图，在平面直角坐标系中，点A（0，4），B（3，0），连接AB，将△AOB沿过点B的直线折叠，使点A落在x轴上的点A′处，折痕所在的直线交y轴正半轴于点C，则直线BC的解析式为　 　．

     

     

    查看答案和解析>>

    科目：初中数学 来源：2014年初中毕业升学考试（黑龙江牡丹江卷）数学（解析版） 题型：选择题

    如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB，CD交于点E，F，连接BF交AC于点M，连接DE，BO．若∠COB=60°，FO=FC，则下列结论：

    ①FB⊥OC，OM=CM；

    ②△EOB≌△CMB；

    ③四边形EBFD是菱形；

    ④MB：OE=3：2．

    其中正确结论的个数是（ ）

    A．1 B．2 C．3 D．4

     

    查看答案和解析>>

    科目：初中数学 来源：2014年初中毕业升学考试（黑龙江牡丹江卷）数学（解析版） 题型：选择题

    在函数y=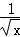中，自变量x的取值范围是（ ）

    A．x≥0 B．x＞0 C．x≠0 D．x＞0且x≠1

     

    查看答案和解析>>

    科目：初中数学 来源：2014年初中毕业升学考试（黑龙江大庆卷）数学（解析版） 题型：填空题

    二元一次方程组的解为　

     

    查看答案和解析>>

    科目：初中数学 来源：2014年初中毕业升学考试（青海西宁卷）数学（解析版） 题型：解答题

    如图，抛物线y=－x2+x－2交x轴于A，B两点（点A在点B的左侧），交y轴于点C，分别过点B，C作y轴，x轴的平行线，两平行线交于点D，将△BDC绕点C逆时针旋转，使点D旋转到y轴上得到△FEC，连接BF．

    （1）求点B，C所在直线的函数解析式；

    （2）求△BCF的面积；

    （3）在线段BC上是否存在点P，使得以点P，A，B为顶点的三角形与△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．

     

     

    查看答案和解析>>

    同步练习册答案