
如图,抛物线y=- x2+
x2+ x-2交x轴于A,B两点(点A在点B的左侧),交y轴于点C,分别过点B,C作y轴,x轴的平行线,两平行线交于点D,将△BDC绕点C逆时针旋转,使点D旋转到y轴上得到△FEC,连接BF.
x-2交x轴于A,B两点(点A在点B的左侧),交y轴于点C,分别过点B,C作y轴,x轴的平行线,两平行线交于点D,将△BDC绕点C逆时针旋转,使点D旋转到y轴上得到△FEC,连接BF.
(1)求点B,C所在直线的函数解析式;
(2)求△BCF的面积;
(3)在线段BC上是否存在点P,使得以点P,A,B为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.

(1)直线BC的解析式为y=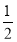 x﹣3;
x﹣3;
(2)△BCF的面积为10;
(3)在线段BC上存在点P,使得以点P,A,B为顶点的三角形与△BOC相似, P点坐标为(2,﹣1)或(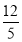 ,﹣
,﹣ ).
).
【解析】
试题分析:(1)根据坐标轴上点的坐标特征可得点B,C的坐标,再根据待定系数法可得点B,C所在直线的函数解析式;
(2)根据勾股定理可得BC的长,根据旋转的性质和三角形面积公式即可求解;
(3)存在.分两种情况讨论:①过A作AP1⊥x轴交线段BC于点P1,则△BAP1∽△BOC;②过A作AP2⊥BC,垂足点P2,过点P2作P2Q⊥x轴于点Q.则△BAP2∽△BCO;依此讨论即可求解.
试题解析:(1)当y=0时,﹣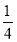 x2+
x2+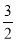 x﹣2=0,
x﹣2=0,
解得x1=2,x2=4,
∴点A,B的坐标分别为(2,0),(4,0),
当x=0时,y=﹣2,
∴C点的坐标分别为(0,﹣2),
设直线BC的解析式为y=kx+b(k≠0),则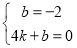 ,
,
解得 .
.
∴直线BC的解析式为y=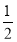 x﹣3;
x﹣3;
(2)∵CD∥x轴,BD∥y轴,
∴∠ECD=90°,
∵点B,C的坐标分别为(4,0),(0,﹣2),
∴BC=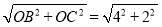 =2
=2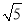 ,
,
∵△FEC是由△BDC绕点C逆时针旋转得到,
∴△BCF的面积=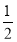 BC•FC=
BC•FC=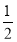 ×2
×2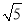 ×2
×2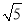 =10;
=10;
(3)存在.分两种情况讨论:
①过A作AP1⊥x轴交线段BC于点P1,则△BAP1∽△BOC,
∵点A的坐标为(2,0),
∴点P1的横坐标是2,
∵点P1在点BC所在直线上,
∴y=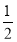 x﹣2=
x﹣2=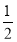 ×2﹣2=﹣1,
×2﹣2=﹣1,
∴点P1的坐标为(2,﹣1);
②过A作AP2⊥BC,垂足点P2,过点P2作P2Q⊥x轴于点Q.
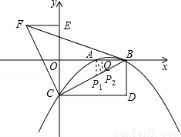
∴△BAP2∽△BCO,
∴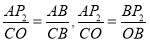 ,
,
∴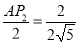 ,
,
解得AP2=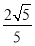 ,
,
∵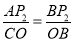 ,
,
∴AP2•BP=CO•BP2,
∴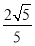 ×4=2BP2,
×4=2BP2,
解得BP2=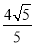 ,
,
∵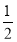 AB•QP2=
AB•QP2=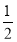 AP2•BP2,
AP2•BP2,
∴2QP2=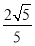 ×
×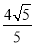 ,
,
解得QP2= ,
,
∴点P2的纵坐标是﹣ ,
,
∵点P2在BC所在直线上,
∴x=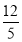 ,
,
∴点P2的坐标为(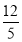 ,﹣
,﹣ ),
),
∴满足条件的P点坐标为(2,﹣1)或(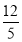 ,﹣
,﹣ ).
).
考点:二次函数综合题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014年初中毕业升学考试(黑龙江牡丹江卷)数学(解析版) 题型:填空题
⊙O的半径为2,弦BC=2 ,点A是⊙O上一点,且AB=AC,直线AO与BC交于点D,则AD的长为 .
,点A是⊙O上一点,且AB=AC,直线AO与BC交于点D,则AD的长为 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(黑龙江大庆卷)数学(解析版) 题型:选择题
下列式子中成立的是( )
A.-|-5|>4 B.-3<|-3| C.-|-4|=4 D.|- 5.5|<5
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(黑龙江哈尔滨卷)数学(解析版) 题型:选择题
在反比例函数 的图象的每一条曲线上,y都随x的增大而减小,则k的取值范围是( )
的图象的每一条曲线上,y都随x的增大而减小,则k的取值范围是( )
A.k>1 B.k>0 C.k≥1 D.k<1
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(青海西宁卷)数学(解析版) 题型:解答题
如图,已知?ABCD水平放置在平面直角坐标系xOy中,若点A,D的坐标分别为(-2,5),(0,1),点B(3,5)在反比例函数y= (x>0)图象上.
(x>0)图象上.
(1)求反比例函数y= 的解析式;
的解析式;
(2)将?ABCD沿x轴正方向平移10个单位后,能否使点C落在反比例函数y= 的图象上?并说明理由.
的图象上?并说明理由.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(重庆A卷)数学(解析版) 题型:解答题
如图,抛物线 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG= DQ,求点F的坐标.
DQ,求点F的坐标.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(辽宁阜新卷)数学(解析版) 题型:选择题
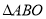 与
与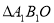 在平面直角坐标系中的位置如图所示,它们关于点
在平面直角坐标系中的位置如图所示,它们关于点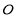 成中心对称,其中点
成中心对称,其中点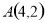 ,则点
,则点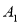 的坐标是( )
的坐标是( )

A.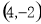 B.
B.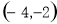 C.
C.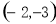 D.
D.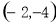
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com