
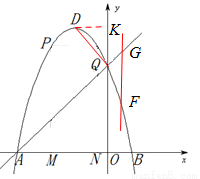
如图,抛物线 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG= DQ,求点F的坐标.
DQ,求点F的坐标.

(1)A(-3,0),B(1,0),C(0,3); (2) ;(3)
;(3)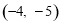 或(1,0).
或(1,0).
【解析】
试题分析:(1)依据抛物线的解析式直接求得C的坐标,令y=0解方程即可求得A、B点的坐标.
(2)求出矩形PQMN的周长关于点M横坐标的解析式,应用二次函数最值原理求出矩形PQMN的周长时点M横坐标的值,求出此时△AEM的面积.
(3)根据FG=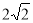 DQ列关于点F横坐标的方程求解即可.
DQ列关于点F横坐标的方程求解即可.
试题解析:(1)由抛物线的解析式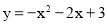 令
令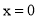 得
得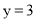 ,∴C(0,3).
,∴C(0,3).
令y=0,-x2+2x+3=0,解得x=-3或x=1.∴A(-3,0),B(1,0).
(2)∵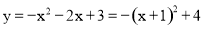 ,∴对称轴为x=-1.
,∴对称轴为x=-1.
设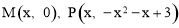 ,其中
,其中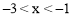 .
.
∵点P、Q关于直线x=-1对称,设点Q的横坐标为a,
则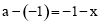 ,∴
,∴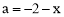 .∴
.∴ 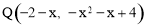 .
.
∴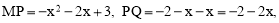
∴矩形PQMN的周长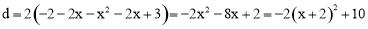 .
.
∴当x=-2时,矩形PQMN的周长d最大.
此时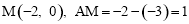 .
.
设直线AC的解析式为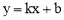 ,则
,则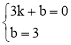 ,解得
,解得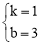 .
.
∴直线AC的解析式为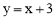 .
.
将x=-2代入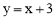 ,得y=1,∴
,得y=1,∴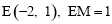 .
.
∴ .
.
(3)由(2)知,当矩形PQMN的周长最大时,x=-2,
此时,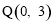 ,与点C重合,∴OQ=3.
,与点C重合,∴OQ=3.
由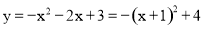 得
得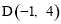 .
.
如图,过点D作DK⊥y轴于点K,则DK=1,OK=4,∴QK=OK-OQ=4-3=1.
∴△DKQ是等腰直角三角形,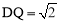 .
.
∴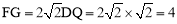 .
.
设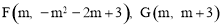 ,则
,则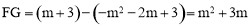 ,
,
∴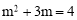 ,解得
,解得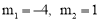 .
.
当 时,
时,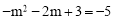 ;当
;当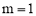 时,
时,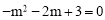 .
.
∴点F的坐标为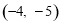 或(1,0).
或(1,0).
考点:1.二次函数综合题;2.单动点问题;3.曲线上点的坐标与方程的关系;4.三角形面积的确定;5.二次函数最值的应用;6.数形结合思想的应用.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2014年初中毕业升学考试(青海西宁卷)数学(解析版) 题型:解答题
如图,抛物线y=- x2+
x2+ x-2交x轴于A,B两点(点A在点B的左侧),交y轴于点C,分别过点B,C作y轴,x轴的平行线,两平行线交于点D,将△BDC绕点C逆时针旋转,使点D旋转到y轴上得到△FEC,连接BF.
x-2交x轴于A,B两点(点A在点B的左侧),交y轴于点C,分别过点B,C作y轴,x轴的平行线,两平行线交于点D,将△BDC绕点C逆时针旋转,使点D旋转到y轴上得到△FEC,连接BF.
(1)求点B,C所在直线的函数解析式;
(2)求△BCF的面积;
(3)在线段BC上是否存在点P,使得以点P,A,B为顶点的三角形与△BOC相似?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(青海西宁卷)数学(解析版) 题型:选择题
一次英语测试后,随机抽取九年级某班5名学生的成绩如下:91,78,98,85,98.关于这组数据说法正确的是( )
A.中位数是91 B.平均数是91 C.众数是91 D.极差是78
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(重庆A卷)数学(解析版) 题型:解答题
如图,△ABC中,AD⊥BC,垂足是D,若BC=14,AD=12.tan∠BAD= ,求sinC的值.
,求sinC的值.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(辽宁阜新卷)数学(解析版) 题型:解答题
如图,在边长为1的正方形组成的网格中, 的顶点均在格点上,其中点
的顶点均在格点上,其中点 ,将
,将 绕点
绕点 逆时针旋转
逆时针旋转 后得到
后得到 .
.
(1)画出 ;
;
(2)在旋转过程中点 所经过的路径长为 ;
所经过的路径长为 ;
(3)求在旋转过程中线段 扫过的图形的面积之和.
扫过的图形的面积之和.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com