
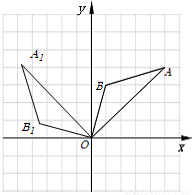
如图,在边长为1的正方形组成的网格中, 的顶点均在格点上,其中点
的顶点均在格点上,其中点 ,将
,将 绕点
绕点 逆时针旋转
逆时针旋转 后得到
后得到 .
.
(1)画出 ;
;
(2)在旋转过程中点 所经过的路径长为 ;
所经过的路径长为 ;
(3)求在旋转过程中线段 扫过的图形的面积之和.
扫过的图形的面积之和.

(1)画图见解析
点B所经过的路径长为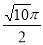 ;
;
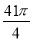
【解析】
试题分析:(1)按要求画出图形即可;
(2)在旋转过程中点B所经过的路径长就是以点O为圆心,以OB长为半径形成的扇形OBB1的弧BB1的长;
(3)在旋转过程中,线段AB,BO扫过的图形的面积之和为以点O为圆心,OA为半径,∠AOA 1为圆心角的扇形面积,因此只要求出扇形OAA1的面积即可.
试题解析:(1)如图;
(2)由图形可知OB=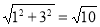 ,点B所经过的路径长为
,点B所经过的路径长为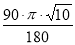 =
=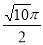 ;
;
(3)由勾股定理可知OA=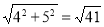
∵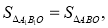
∴在旋转过程中,线段AB,BO扫过的图形的面积之和为以点O为圆心,OA为半径,∠AOA 1为圆心角的扇形面积.
∴ 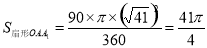 .
.
考点:1、旋转;2、扇形的弧长;3、扇形的面积.


科目:初中数学 来源:2014年初中毕业升学考试(重庆A卷)数学(解析版) 题型:解答题
如图,抛物线 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG= DQ,求点F的坐标.
DQ,求点F的坐标.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(重庆A卷)数学(解析版) 题型:选择题
如图,直线AB∥CD,直线EF分别交直线AB、CD于点E、F,过点F作FG⊥FE,交直线AB于点G.若∠1=42°,则∠2的大小是( )

A.56° B.48° C.46° D.40°
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(辽宁阜新卷)数学(解析版) 题型:选择题
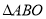 与
与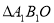 在平面直角坐标系中的位置如图所示,它们关于点
在平面直角坐标系中的位置如图所示,它们关于点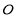 成中心对称,其中点
成中心对称,其中点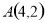 ,则点
,则点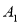 的坐标是( )
的坐标是( )

A.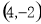 B.
B.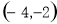 C.
C.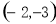 D.
D.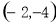
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(辽宁抚顺卷)数学(解析版) 题型:填空题
把标号分别为a,b,c的三个小球(除标号外,其余均相同)放在一个不透明的口袋中,充分混合后,随机地摸出一个小球,记下标号后放回,充分混合后,再随机地摸出一个小球,两次摸出的小球的标号相同的概率是 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(贵州贵阳卷)数学(解析版) 题型:解答题
如图,将一副直角三角形拼放在一起得到四边形ABCD,其中∠BAC=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点.若AB=6 cm.
cm.
(1)AE的长为 cm;
(2)试在线段AC上确定一点P,使得DP+EP的值最小,并求出这个最小值;
(3)求点D′到BC的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com