
如图,在坐标系xOy中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线 的图象过C点.
的图象过C点.
(1)求抛物线的解析式;
(2)平移该抛物线的对称轴所在直线l.当l移动到何处时,恰好将△ABC的面积分为相等的两部分?
(3)点P是抛物线上一动点,是否存在点P,使四边形PACB为平行四边形?若存在,求出P点坐标;若不存在,说明理由.
解:(1)如答图1所示,过点C作CD⊥x轴于点D,则∠CAD+∠ACD=90°。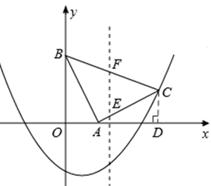
∵∠OBA+∠OAB=90°,∠OAB+∠CAD=90°,
∴∠OAB=∠ACD,∠OBA=∠CAD。
∵在△AOB与△CDA中,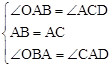 ,
,
∴△AOB≌△CDA(ASA)。
∴CD=OA=1,AD=OB=2。
∴OD=OA+AD=3。
∴C(3,1)。
∵点C(3,1)在抛物线 上,
上,
∴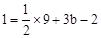 ,解得:
,解得: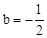 。
。
∴抛物线的解析式为: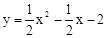 。
。
(2)在Rt△AOB中,OA=1,OB=2,由勾股定理得:AB=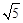 。
。
∴S△ABC= AB2=
AB2=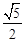 。
。
设直线BC的解析式为y=kx+b,∵B(0,2),C(3,1),
∴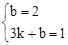 ,解得
,解得 。
。
∴直线BC的解析式为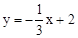 。
。
同理求得直线AC的解析式为: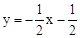 。
。
如答图1所示,设直线l与BC、AC分别交于点E、F,
则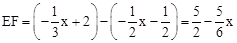 。
。
在△CEF中,CE边上的高h=OD﹣x=3﹣x.
由题意得:S△CEF= S△ABC,即:
S△ABC,即: EF•h=
EF•h= S△ABC。
S△ABC。
∴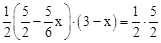 ,整理得:(3﹣x)2=3。
,整理得:(3﹣x)2=3。
解得x=3﹣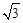 或x=3+
或x=3+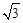 (不合题意,舍去)。
(不合题意,舍去)。
∴当直线l解析式为x=3﹣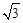 时,恰好将△ABC的面积分为相等的两部分。
时,恰好将△ABC的面积分为相等的两部分。
(3)存在。如答图2所示,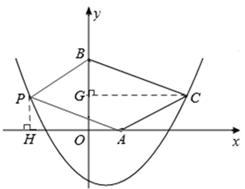
过点C作CG⊥y轴于点G,则CG=OD=3,OG=1,BG=OB﹣OG=1。
过点A作AP∥BC,且AP=BC,连接BP,则四边形PACB为平行四边形。
过点P作PH⊥x轴于点H,
则易证△PAH≌△BCG。
∴PH=BG=1,AH=CG=3,∴OH=AH﹣OA=2。
∴P(﹣2,1)。
∵抛物线解析式为: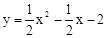 ,当x=﹣2时,y=1,即点P在抛物线上。
,当x=﹣2时,y=1,即点P在抛物线上。
∴存在符合条件的点P,点P的坐标为(﹣2,1).。
解析


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
已知抛物线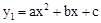 a≠0)的对称轴是直线l,顶点为点M.若自变量x和函数值y1的部分对应值如下表所示:
a≠0)的对称轴是直线l,顶点为点M.若自变量x和函数值y1的部分对应值如下表所示:
| x | … | ―1 | 0 | 3 | … |
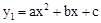 | … | 0 |  | 0 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点,与x轴交于另一个点C,对称轴与直线AB交于点E,抛物线顶点为D.
(1)求抛物线的解析式;
(2)在第三象限内,F为抛物线上一点,以A、E、F为顶点的三角形面积为3,求点F的坐标;
(3)点P从点D出发,沿对称轴向下以每秒1个单位长度的速度匀速运动,设运动的时间为t秒,当t为何值时,以P、B、C为顶点的三角形是直角三角形?直接写出所有符合条件的t值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,已知抛物线y=ax2+bx+c与x轴的一个交点A的坐标为(﹣1,0),对称轴为直线x=﹣2.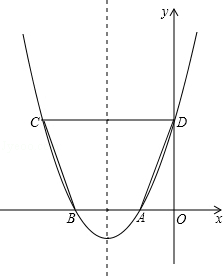
(1)求抛物线与x轴的另一个交点B的坐标;
(2)点D是抛物线与y轴的交点,点C是抛物线上的另一点.已知以AB为一底边的梯形ABCD的面积为9.求此抛物线的解析式,并指出顶点E的坐标;
(3)点P是(2)中抛物线对称轴上一动点,且以1个单位/秒的速度从此抛物线的顶点E向上运动.设点P运动的时间为t秒.
①当t为 秒时,△PAD的周长最小?当t为 秒时,△PAD是以AD为腰的等腰三角形?(结果保留根号)
②点P在运动过程中,是否存在一点P,使△PAD是以AD为斜边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在直角梯形AOCB中,AB∥OC,∠AOC=90°,AB=1,AO=2,OC=3,以O为原点,OC、OA所在直线为轴建立坐标系.抛物线顶点为A,且经过点C.点P在线段AO上由A向点O运动,点O在线段OC上由C向点O运动,QD⊥OC交BC于点D,OD所在直线与抛物线在第一象限交于点E.
(1)求抛物线的解析式;
(2)点E′是E关于y轴的对称点,点Q运动到何处时,四边形OEAE′是菱形?
(3)点P、Q分别以每秒2个单位和3个单位的速度同时出发,运动的时间为t秒,当t为何值时,PB∥OD?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为鼓励大学毕业生自主创业,某市政府出台了相关政策:由政府协调,本市企业按成本价提供产品给大学毕业生自主销售,成本价与出厂价之间的差价由政府承担.李明按照相关政策投资销售本市生产的一种新型节能灯.已知这种节能灯的成本价为每件10元,出厂价为每件12元,每月销售量y(件)与销售单价x(元)之间的关系近似满足一次函数:y=﹣10x+500.
(1)李明在开始创业的第一个月将销售单价定为20元,那么政府这个月为他承担的总差价为多少元?
(2)设李明获得的利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(3)物价部门规定,这种节能灯的销售单价不得高于25元.如果李明想要每月获得的利润不低于300元,那么政府为他承担的总差价最少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(2013年四川眉山11分)如图,在平面直角坐标系中,点A、B在x轴上,点C、D在y轴上,且OB=OC=3,OA=OD=1,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点,直线AD与抛物线交于另一点M.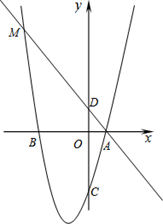
(1)求这条抛物线的解析式;
(2)P为抛物线上一动点,E为直线AD上一动点,是否存在点P,使以点A、P、E为顶点的三角形为等腰直角三角形?若存在,请求出所有点P的坐标;若不存在,请说明理由.
(3)请直接写出将该抛物线沿射线AD方向平移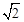 个单位后得到的抛物线的解析式.
个单位后得到的抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(2013年广东梅州10分)如图,已知抛物线y=2x2﹣2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C.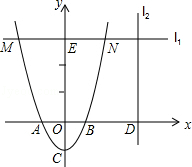
(1)写出以A,B,C为顶点的三角形面积;
(2)过点E(0,6)且与x轴平行的直线l1与抛物线相交于M、N两点(点M在点N的左侧),以MN为一边,抛物线上的任一点P为另一顶点做平行四边形,当平行四边形的面积为8时,求出点P的坐标;
(3)过点D(m,0)(其中m>1)且与x轴垂直的直线l2上有一点Q(点Q在第一象限),使得以Q,D,B为顶点的三角形和以B,C,O为顶点的三角形相似,求线段QD的长(用含m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某校为培育青少年科技创新能力,举办了动漫制作活动,小明设计了点做圆周运动的一个雏形,如图所示,甲、乙两点分别从直径的两端点A、B以顺时针、逆时针的方向同时沿圆周运动,甲运动的路程l(cm)与时间t(s)满足关系: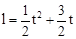 (t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.
(t≥0),乙以4cm/s的速度匀速运动,半圆的长度为21cm.
(1)甲运动4s后的路程是多少?
(2)甲、乙从开始运动到第一次相遇时,它们运动了多少时间?
(3)甲、乙从开始运动到第二次相遇时,它们运动了多少时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com