练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．下列关于单项式$-\frac{{3x{y^2}}}{5}$的说法中，正确的是（　　）
    A．系数是3，次数是2B．系数是$-\frac{3}{5}$，次数是2
    C．系数是$\frac{3}{5}$，次数是3D．系数是$-\frac{3}{5}$，次数是3

    分析 根据单项式的概念即可判断．

    解答 解：单项式$-\frac{{3x{y^2}}}{5}$的系数为-$\frac{3}{5}$，次数为3，
    故选（D）

    点评 本题考查单项式的概念，属于基础题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

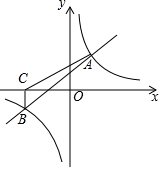    8．如图，一次函数y=x+2与反比例函数y=$\frac{k}{x}$的图象相交于A（2，m），B（-4，n）两点．
    （1）求反比例函数的解析式；
    （2）根据所给条件，请直接写出不等式x+2＞$\frac{k}{x}$的解集：-4＜x＜0或x＞2；
    （3）过点B作BC⊥x轴，垂足为C，连接AC，求S△ABC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

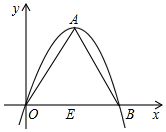    9．如果一条抛物线y=ax2+bx+c（a≠0）与x轴有两个交点，那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”．
    （1）请你判定“抛物线三角形”的形状（不必写出证明过程）；
    （2）若抛物线y=-x2+bx（b＞0）的“抛物线三角形”是等腰直角三角形，求b的值；
    （3）如图，△OAB是抛物线y=-x2+b′x（b′＞0）的“抛物线三角形”．请问是否存在以原点O为对称中心的矩形ABCD？若存在，求出过O、C、D三点的抛物线的表达式；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

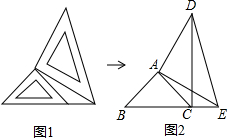    6．如图，两个大小不同的等腰直角三角形三角板如图1所示放置，图2是由它抽象出的几何图形，B，C，E在同一条直线上，连结DC．请找出图2中的全等三角形，并给予证明（不再添加其它线段，不再标注或使用其它字母）．
    解：（1）你找到的全等三角形是：△ABE≌△ACD；
    （2）证明：$\frac{{x}^{2}+1}{{x}^{2}-1}$-$\frac{x-2}{x-1}$÷$\frac{x-2}{x}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．在一次朋友聚餐中，有A、B、C、D四种素菜可供选择，小明从中选择一种，小莉也从中选择一种（与小明选择的不相同），请利用列表或树状图的方法求出A与B两种素菜被选中的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．解方程：
    （1）3（x-4）=3-2x
    （2）$\frac{x+1}{2}$-$\frac{2-3x}{6}$=1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．实数a，b，c，d在数轴上对应点的位置如图所示，这四个数中，绝对值最小的是（　　）
    A．aB．bC．cD．d

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

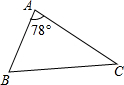    7．如图，△ABC中，∠A=78°，AB=4，AC=6．将△ABC沿图中的虚线剪开，剪下的阴影三角形与原三角形不相似的是（　　）
    A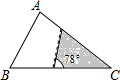．B．C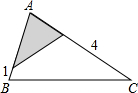．D．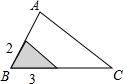

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．计算：$\frac{2}{b}$$\sqrt{a{b}^{5}}$÷$\frac{6a}{{b}^{2}}$$\sqrt{\frac{b}{a}}$×（-$\frac{3}{2}$$\sqrt{{a}^{3}b}$）

    查看答案和解析>>

    同步练习册答案