
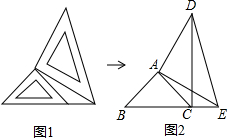
 如图,两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.请找出图2中的全等三角形,并给予证明(不再添加其它线段,不再标注或使用其它字母).
如图,两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.请找出图2中的全等三角形,并给予证明(不再添加其它线段,不再标注或使用其它字母).分析 (1)根据图形得出答案即可;
(2)根据等腰直角三角形得出AB=AC,AE=AD,∠BAC=∠DAE=90°,求出∠BAE=∠DAC,根据全等三角形的判定推出即可.
解答 解:(1)全等三角形为:△ABE≌△ACD;故答案为:△ABE≌△ACD;
(2)证明如下:
∵△ABE和△DAE是等腰直角三角形,
∴AB=AC,AE=AD,∠BAC=∠DAE=90°,
∴∠BAC+∠CAE=∠DAE+∠CAE,
∴∠BAE=∠DAC,
在△ABE和△ACD中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAE=∠DAC}\\{AE=AD}\end{array}\right.$,
∴△ABE≌△ACD(SAS).
点评 本题考查了等腰直角三角形,全等三角形的判定的应用,解此题的关键是推出判定两三角形全等的三个条件.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
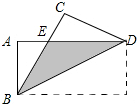 如图,把长方形ABCD沿对角线BD折叠,重合部分为△EBD.
如图,把长方形ABCD沿对角线BD折叠,重合部分为△EBD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
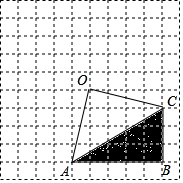 如图,在网格中有一个四边形图案.
如图,在网格中有一个四边形图案.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知AC是矩形ABCD的对角线,过AC的中点O的直线EF,交BC于点F,交BC于点F,交AD于点E,连接AF,CE.
如图,已知AC是矩形ABCD的对角线,过AC的中点O的直线EF,交BC于点F,交BC于点F,交AD于点E,连接AF,CE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 系数是3,次数是2 | B. | 系数是$-\frac{3}{5}$,次数是2 | ||
| C. | 系数是$\frac{3}{5}$,次数是3 | D. | 系数是$-\frac{3}{5}$,次数是3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
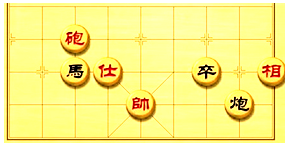 象棋在中国有着三千多年的历史,属于二人对抗性游戏的一种.由于用具简单,趣味性强,成为流行极为广泛的棋艺活动.如图是一方的棋盘,如果“马”的坐标是(-2,2),它是抛物线y=ax2(a≠0)上的一个点,那么下面哪个棋子在该抛物线上( )
象棋在中国有着三千多年的历史,属于二人对抗性游戏的一种.由于用具简单,趣味性强,成为流行极为广泛的棋艺活动.如图是一方的棋盘,如果“马”的坐标是(-2,2),它是抛物线y=ax2(a≠0)上的一个点,那么下面哪个棋子在该抛物线上( )| A. | 帥 | B. | 卒 | C. | 炮 | D. | 仕 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com