
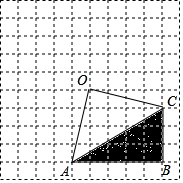
 如图,在网格中有一个四边形图案.
如图,在网格中有一个四边形图案.分析 (1)根据图形旋转的性质画出旋转后的三角形即可;
(2)观察画出的图形,可发现S四边形AA1A2A3=S四边形AB1B2B3-4S△BAA3依次代入求值;
(3)这个图案就是我们几何中的著名的勾股定理.
解答 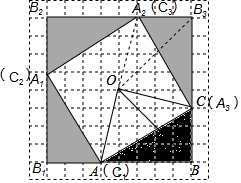 解:(1)如图,正确画出图案;
解:(1)如图,正确画出图案;
(2)如图,S四边形AA1A2A3=S四边形BB1B2B3-4S△BAA3
=(3+5)2-4×$\frac{1}{2}$×3×5,
=34(1分)
故四边形AA1A2A3的面积为34.
(3)由图可知:(a+c)2=4×$\frac{1}{2}$ac+b2,
整理得:c2+a2=b2,
即:AB2+BC2=AC2.
这就是著名的勾股定理.
点评 本题考查的是利用旋转设计图案,注意:找旋转对应点是做这类题的关键.看图是关键.比如第二小题就要通过看图得出面积.所以学生所学过的知识还要融汇贯通.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )
一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
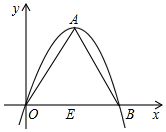 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
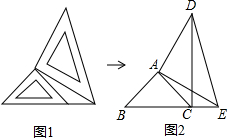 如图,两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.请找出图2中的全等三角形,并给予证明(不再添加其它线段,不再标注或使用其它字母).
如图,两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.请找出图2中的全等三角形,并给予证明(不再添加其它线段,不再标注或使用其它字母).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com