【题目】按“有无曲面”将下列几何体分类则与其他三个几何体不相同的一个是（ ）
A.圆柱B.圆锥C.球D.立方体
科目：初中数学 来源： 题型：
【题目】如图四边形ABCD是菱形，且∠ABC=60，△ABE是等边三角形，M为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM，则下列五个结论中正确的是（ ）
①若菱形ABCD的边长为1，则AM+CM的最小值1；
②△AMB≌△ENB；
③S四边形AMBE=S四边形ADCM；
④连接AN，则AN⊥BE；
⑤当AM+BM+CM的最小值为2
时，菱形ABCD的边长为2．
A. ①②③ B. ②④⑤ C. ①②⑤ D. ②③⑤
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知两条射线OM∥CN，动线段AB的两个端点A、B分别在射线OM、CN上，且∠C=∠OAB=108°，F在线段CB上，OB平分∠AOF，OE平分∠COF．
（1）请在图中找出与∠AOC相等的角，并说明理由；
（2）若平行移动AB，那么∠OBC与∠OFC的度数比是否随着AB位置的变化而发生变化？若变化，找出变化规律；若不变，求出这个比值；
（3）在平行移动AB的过程中，是否存在某种情况，使∠OEC=2∠OBA？若存在，请求出∠OBA度数；若不存在，说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在边长为4的菱形ABCD中，BD=4，E、F分别是AD、CD上的动点（包含端点），且AE+CF=4，连接BE、EF、FB．
（1）试探究BE与BF的数量关系，并证明你的结论；
（2）求EF的最大值与最小值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如果一个分式的分子或分母可以因式分解，且这个分式不可约分，那么我们称这
个分式为“和谐分式”.
（1）下列分式:①
；②
；③
；④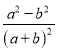
. 其中是“和谐分式”是 (填写序号即可)；
（2）若
为正整数，且
为“和谐分式”，请写出
的值;
（3）在化简
时，
小东和小强分别进行了如下三步变形:
小东： 
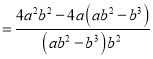
小强： 
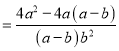
显然，小强利用了其中的和谐分式, 第三步所得结果比小东的结果简单，
原因是： ，
请你接着小强的方法完成化简.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直角坐标系中，△ABC的顶点都在网格点上，其中，C点坐标为（1，2）．
（1）写出点A、B的坐标:
（2）将△ABC先向左平移2个单位长度，再向上平移1个单位长度，得到△A′B′C′，画出△A′B′C′；
（3）若AB边上有一点M（a，b），平移后对应的点M′的坐标为:
（4）求△ABC的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在下面直角坐标系中，已知A（0，a），B（b，0），C（b，c）三点，其中a、b、c满足关系式
+（b﹣3）2=0，（c﹣4）2≤0
（1）求a、b、c的值；
（2）如果在第二象限内有一点P（﹣m，
），请用含m的式子表示四边形ABOP的面积；
（3）在（2）的条件下，是否存在点P，使四边形ABOP的面积与△ABC的面积相等？若存在，求出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙、丙、丁四支足球队进行小组单循环比赛（每两队都要比赛一场），结果甲队胜了丙队，并且甲、乙、丁胜的场数相同，则这三队各胜的场数是（ ）
A.3B.2C.1D.0
查看答案和解析>>
科目：初中数学 来源： 题型：
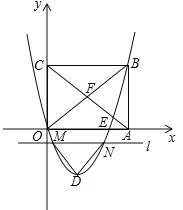
【题目】如图，在平面直角坐标系中，矩形OABC的边OA、OC分别在x轴、y轴上，点B坐标为（4，t）（t＞0），二次函数
（b＜0）的图象经过点B，顶点为点D．
（1）当t=12时，顶点D到x轴的距离等于 ；
（2）点E是二次函数
（b＜0）的图象与x轴的一个公共点（点E与点O不重合），求OEEA的最大值及取得最大值时的二次函数表达式；
（3）矩形OABC的对角线OB、AC交于点F，直线l平行于x轴，交二次函数
（b＜0）的图象于点M、N，连接DM、DN，当△DMN≌△FOC时，求t的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
