Question

如图，在△ABC中，D为AB上一点，⊙O经过B、C、D三点，∠COD=90°，∠ACD=∠BCO+∠BDO．
（1）求证：直线AC是⊙O的切线；
（2）若∠BCO=15°，⊙O的半径为2，求BD的长．

Answer 1

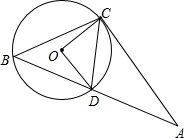
（1）证明：连接OB．
∵∠COD=90°，且∠COD与∠CBD是分别所对的圆心角和圆周角，
∴∠CBD=∠COD=45°，
∵OB=OC，OB=OD，
∴∠OBC=∠BCO，∠OBD=∠BDO，
∵∠CBD=∠OBC+∠OBD=45°，
∴∠BCO+∠BDO=45°，
∵∠ACD=∠BCO+∠BDO，
∴∠ACD=45°，
在Rt△COD中，OC=OD，
∴∠OCD=45°，
∴∠OCA=90°，
∴直线AC是⊙O的切线；

（2）解：过O作OE⊥BD，垂足为E．
∴BD=2DE，
∵∠BCO+∠BDO=45°，∠BCO=15°，
∴∠BDO=30°，
在Rt△DOE中，
DE=OD•cos30°=2×=．
∴BD=2DE=2．
分析：（1）连接OB，首先根据同弧所对的圆周角等于它所对圆心角度数的一半求出∠CBD，即为∠OBC+∠OBD的度数，然后根据等边对等角分别得到∠OBC=∠BCO，∠OBD=∠BDO两对角的相等，等量代换可得到∠BCO+∠BDO的度数，由已知的∠ACD=∠BCO+∠BDO，即可求出∠ACD=45°，再由△OCD为等腰直角三角形可求出∠OCD=45°，从而得到∠OCA=90°，利用经过直径的一端，并且垂直于这条直径的直线是圆的切线可得证；
（2）由（1）中的∠BCO+∠BDD=45°，且∠BCO=15°，求出∠BDO=30°，然后在直角三角形ODE中，根据半径的长及∠BDO的度数，利用30°的余弦值即可求出DE的长，最后根据垂径定理可得BD=2DE求出结果．
点评：此题考查了切线的判定，圆周角定理，等腰三角形的性质，垂径定理，以及锐角三角函数的定义，是一道多知识的综合题，要求学生把所学的知识融汇贯穿，灵活运用，注意利用转化的数学思想．其中证明切线的方法一般有以下两种：①有点连接证明半径（或直径）与所证的直线垂直；②无点作垂线，证明圆心到直线的距离等于半径．