
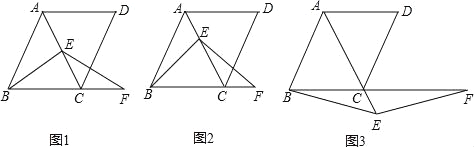
【题目】在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
(1)如图1,当E是线段AC的中点时,求证:BE=EF.
(2)如图2,当点E不是线段AC的中点,其它条件不变时,请你判断(1)中的结论: .(填“成立”或“不成立”)
(3)如图3,当点E是线段AC延长线上的任意一点,其它条件不变时,(1)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.
【答案】(1)证明见解析;(2)成立;(3)成立.证明见解析.
【解析】
试题分析:(1)由菱形的性质和已知条件得出△ABC是等边三角形,得出∠BCA=60°,由等边三角形的性质和已知条件得出CE=CF,由等腰三角形的性质和三角形的外角性质得出∠CBE=∠F,即可得出结论;
(2)过点E作EG∥BC交AB延长线于点G,先证明△ABC是等边三角形,得出AB=AC,∠ACB=60°,再证明△AGE是等边三角形,得出AG=AE=GE,∠AGE=60°,然后证明
△BGE≌△ECF,即可得出结论;
(3)过点E作EG∥BC交AB延长线于点G,证明同(2).
试题解析:(1)∵四边形ABCD是菱形,
∴AB=BC,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴∠BCA=60°,
∵E是线段AC的中点,
∴∠CBE=∠ABE=30°,AE=CE,
∵CF=AE,
∴CE=CF,
∴∠F=∠CEF=![]() ∠BCA=30°,
∠BCA=30°,
∴∠CBE=∠F=30°,
∴BE=EF;
(2)结论成立;理由如下:
过点E作EG∥BC交AB于点G,如图2所示:
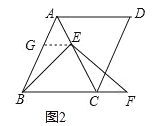
∵四边形ABCD为菱形,
∴AB=BC,∠BCD=120°,AB∥CD,
∴∠ACD=60°,∠DCF=∠ABC=60°,
∴∠ECF=120°,
又∵∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC,∠ACB=60°,
又∵EG∥BC,
∴∠AGE=∠ABC=60°,
又∵∠BAC=60°,
∴△AGE是等边三角形,
∴AG=AE=GE,∠AGE=60°,
∴BG=CE,∠BGE=120°=∠ECF,
又∵CF=AE,
∴GE=CF,
在△BGE和△CEF中,
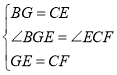 ,
,
∴△BGE≌△ECF(SAS),
∴BE=EF.
(3)结论成立.证明如下:
过点E作EG∥BC交AB延长线于点G,如图3所示:
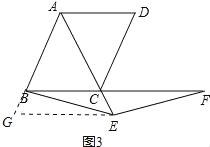
∵四边形ABCD为菱形,
∴AB=BC,
又∵∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC,∠ACB=60°,
∴∠ECF=60°,
又∵EG∥BC,
∴∠AGE=∠ABC=60°,
又∵∠BAC=60°,
∴△AGE是等边三角形,
∴AG=AE=GE,∠AGE=60°,
∴BG=CE,∠AGE=∠ECF,
又∵CF=AE,
∴GE=CF,
在△BGE和△CEF中,
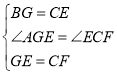 ,
,
∴△BGE≌△ECF(SAS),
∴BE=EF.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,一条抛物线与x轴相交于A、B两点,其顶点P在折线C-D-E上移动,若点C、D、E的坐标分别为(-1,4)、(3,4)、(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为( )
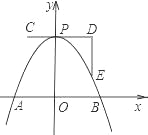
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】面试时,某人的基本知识、表达能力、工作态度的得分分别是90分,80分,85分,若依次按30%,30%,40%的比例确定成绩,则这个人的面试成绩是( )分
A. 75B. 80C. 82D. 85
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=![]() -1与函数y=kx交于点A(2,b)、B(-3,m)两点(点A在第一象限),
-1与函数y=kx交于点A(2,b)、B(-3,m)两点(点A在第一象限),
(1)求b,m,k的值;
(2)函数y=![]() -1与x轴交于点C,求△ABC的面积.
-1与x轴交于点C,求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点的门票价格如表:
购票人数/人 | 1~50 | 51~100 | 100以上 |
每人门票价/元 | 12 | 10 | 8 |
某校七年级(1)、(2)两班计划去游览该景点,其中(1)班人数少于50人,(2)班人数多于50人且少于100人,如果两班都以班为单位单独购票,则一共支付1118元;如果两班联合起来作为一个团体购票,则只需花费816元.
(1)两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com