
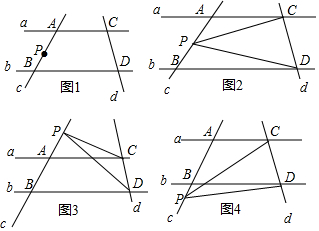
 AB∥CD,MF⊥NF,MF交AB于点E,NF交CD于点G,∠1=140°,则∠2=50度.
AB∥CD,MF⊥NF,MF交AB于点E,NF交CD于点G,∠1=140°,则∠2=50度. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果一件事发生的机会只有千万分之一,那么它就是不可能事件 | |
| B. | 如果一件事发生的机会达99.999%,那么它就是必然事件 | |
| C. | 如果一件事不是不可能事件,那么它就是必然事件 | |
| D. | 如果一件事不是必然事件,那么它就是不可能事件或随机事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
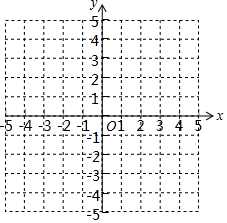 已知A(-3,-2),B(2,-2),C(3,1),D(-2,1)四个点.
已知A(-3,-2),B(2,-2),C(3,1),D(-2,1)四个点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对我国初中学生视力状况的调查 | |
| B. | 对“最强大脑”节目收视率的调查 | |
| C. | 对一批节能灯管使用寿命的调查 | |
| D. | 对量子科学通信卫星上某种零部件的调查 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com