
【题目】如图,在△ABC中,AB=AC=3,∠B=50°,点D在BC边上(不与点B,C重合),连接AD,作∠ADE=50°,DE交边AC于点E.
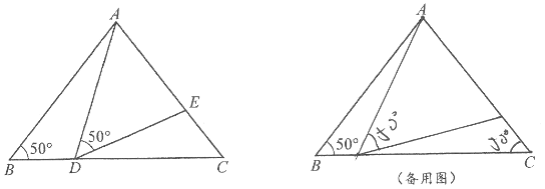
(1)当∠BAD=20°时,求∠CDE的度数;
(2)当CD等于多少时,△ABD≌△DCE?为什么?
(3)在点D运动的过程中,△ADE可能是等腰三角形吗?若可能,直接写出∠DAE的度数;若不可能,说明理由.
【答案】(1)20°;(2)见解析;(3)见解析.
【解析】
(1)利用邻补角的性质和三角形内角和定理解题;
(2)当CD=3时,利用∠B+∠BAD=∠ADE+∠CDE,求出∠BAD=∠CDE,再利用AB=CD=3,∠B=∠C=50°,即可得出△ABD≌△DCE;
(3)△ADE为等腰三角形有三种情况,∠ADE=∠DAC或者∠DAC=∠AED或者∠ADE=∠AED,根据题意排除∠ADE=∠AED的可能.
解:(1)∵∠ADC为三角形ABD的外角.
∴∠B+∠BAD=∠ADE+∠CDE.
∴50°+20°=50°+∠CDE.
∴∠CDE=20°;
(2)CD=3时,△ABD≌△DCE,求证如下:
AB=CD=3,
∵∠B+∠BAD=∠ADE+∠CDE,
由题意知∠B=∠ADE=50°,
∴∠BAD=∠CDE,
又∵AB=AC,△ABC为等腰三角形,
∴∠B=∠C=50°,
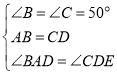 ,
,
∴△ABD≌△DCE(SAS);
(3)△ADE为等腰三角形有三种情况,∠ADE=∠DAC或者∠DAC=∠AED或者∠ADE=∠AED,根据题意排除∠ADE=∠AED的可能,
∵∠C=50°,∠AED肯定大于∠C,
当∠DAE的度数为50°时,
∠BAC=180°-∠B-∠C=80°,
∠BAD=∠CDE=80°-50°=30°,
∠AED=∠C+∠CDE=50°+30°=80°,
∴△ADE的形状是等腰三角形;
∠DAE的度数为65°时,
∠BAD=∠CDE=80°-65°=15°,
∠AED=∠C+∠CDE=50°+15°=65°,
∴△ADE的形状是等腰三角形;
∴三角形ADE为等腰三角形,∠DAE的度数为50°或65°.


科目:初中数学 来源: 题型:
【题目】某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题.
(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆柱的高是![]() ,当圆柱的底面半径
,当圆柱的底面半径![]() 由小到大变化时,圆柱的体积
由小到大变化时,圆柱的体积![]() 也随之发生了变化.
也随之发生了变化.

(1)在这个变化中,自变量是______,因变量是______;
(2)写出体积![]() 与半径
与半径![]() 的关系式;
的关系式;
(3)当底面半径由![]() 变化到
变化到![]() 时,通过计算说明圆柱的体积增加了多少
时,通过计算说明圆柱的体积增加了多少![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
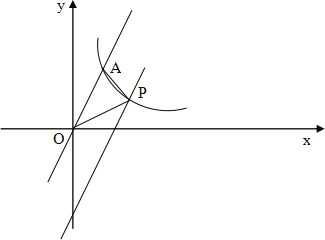
【题目】如图,在平面直角坐标系中,直线y=2x与反比例函数y=![]() 在第一象限内的图像交于点A(m,2),将直线y=2x向下平移后与反比例函数y=
在第一象限内的图像交于点A(m,2),将直线y=2x向下平移后与反比例函数y=![]() 在第一象限内的图像交于点P,且△POA的面积为2.
在第一象限内的图像交于点P,且△POA的面积为2.
(1)求k的值;
(2)求平移后的直线的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图

(1)如图1,学校A,B在道路MN的异侧.在MN上建公交站P,使得P到A,B的距离相等。利用尺规作图确定P的位置.
(2)如图2,学校C,D在道路MN的同侧,在MN上建公交站Q,使得Q到C,D的距离的和最短.利用网格确定Q的位置.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与x轴交于点A、B(点A位于点B左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
与x轴交于点A、B(点A位于点B左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(1)求点A、B、C的坐标;
(2)设动点N(-2,n),求使MN+BN的值最小时n的值;
(3)P是抛物线上位于x轴上方的一点,请探究:是否存在点P,使以P、A、B为顶点的三角形与△ABD相似?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数图象在探索函数的性质中有非常重要的作用,下面我们就一类特殊的函数展开探索,画函数![]() 的图象,经历分析解析式、列表、描点、连线过程得到函数图象如下图所示:
的图象,经历分析解析式、列表、描点、连线过程得到函数图象如下图所示:
| …… | -3 | -2 | -1 | 0 | 1 | 2 | 3 | …… |
| …… | 6 | 4 | 2 | 0 | 2 | 4 | 6 | …… |
经历同样的过程画函数![]() 和
和![]() 的图象如下图所示,观察发现:三个函数的图象都是由两条射线组成的轴对称图形:三个函数解析式中绝对值前面的系数相同,则图象的开口方向和形状完全相同,只有最高点和对称轴发生了变化.
的图象如下图所示,观察发现:三个函数的图象都是由两条射线组成的轴对称图形:三个函数解析式中绝对值前面的系数相同,则图象的开口方向和形状完全相同,只有最高点和对称轴发生了变化.
![]() 请直接写出
请直接写出![]() 与
与![]() 的交点坐标和函数
的交点坐标和函数![]() 的对称轴;
的对称轴;
![]() 在所给的平面直角坐标系内画出函数
在所给的平面直角坐标系内画出函数![]() 的图象(不列表),并写出函数
的图象(不列表),并写出函数![]() 的一条性质;
的一条性质;
![]() 结合函数图像,直接写出不等式
结合函数图像,直接写出不等式![]() 时
时![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com