
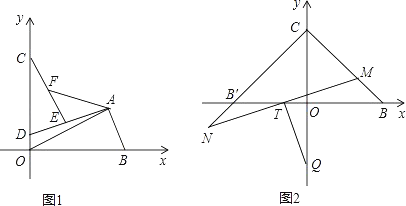
【题目】如图,直角坐标系中,点B(a,0),点C(0,b),点A在第一象限.若a,b满足(a﹣t)2+|b﹣t|=0(t>0).
(1)证明:OB=OC.
(2)如图1,连接AB,过A作AD⊥AB交y轴于D,在射线AD上截取AE=AB,连接CE,F是CE的中点,连接AF,OA,当点A在第一象限内运动(AD不过点C)时,证明:∠OAF的大小不变.
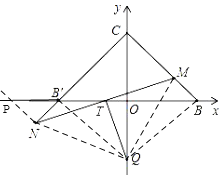
(3)如图2,B′与B关于y轴对称,M在线段BC上,N在CB′的延长线上,且BM=NB′,连接MN交x轴于点T,过T作TQ⊥MN交y轴于点Q,求点Q的坐标.
【答案】(1)证明见解析;(2)证明见解析;(3)Q(0,-t).
【解析】
(1)利用平方和绝对值的非负数性质即可用t表示出a、b,即可得B、C坐标,进而可得答案;(2)如图,延长AF到点P,使PF=AF;连接CP、OP、OF,利用SAS可证明△AEF≌△PCF,可得AE=PC=AB,∠AEF=∠PCF,AE∥PC,由平行线的性质可得∠PCO=∠CDA=180-∠ADO,利用四边形内角和可得∠ABO=180-∠ADO,即可证明∠PCO=∠ABO,利用SAS可证明△PCO≌△ABO,可得OP=OA,∠POC=∠AOB,利用角的和差关系可得∠AOP=∠BOC=90°,即可证明△AOP为等腰直角三角形,可得∠OAF=45°,是定值;(3)过N作NP∥MB,交x轴于P;连接NQ、MQ、BQ、B′Q,由轴对称性质可得BB′=2OB,BC=B′C,可得△BCB′是等腰直角三角形,根据等腰直角三角形的性质及平行线的性质可得∠B′PN=∠PB′N,即可证明NP=NB′=MB,利用AAS可证明△PTN≌△BTM,可得NT=MT,利用SSS可证明△BQM≌△B′QN,可得∠NB′Q=∠MBQ,利用SAS可证明△BCQ≌△B′CQ,可得△OBQ为等腰直角三角形,可得OQ=OB,即可求出Q点坐标.
(1)∵(a-t)≥0,|b-t|≥0,
∴a-t=0,b-t=0,
解得:a=t,b=t
∴B(t,0)、C(0,t)
∴OB=OC
(2)如图,延长AF到点P,使PF=AF;连接CP、OP、OF,
在△AEF和△PCF中,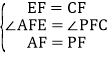
∴△AEF≌△PCF,
∴AE=PC=AB,∠AEF=∠PCF
∴AE∥PC,∠PCO=∠CDA=180-∠ADO
四边形ABOD中,∠ABO=360-∠BOD-∠BAD-∠ADO,
∵∠BOD=90°,AD⊥AB,
∴∠ABO=180-∠ADO,
∴∠PCO=∠ABO
在△PCO和△ABO中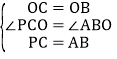 ,
,
∴△PCO≌△ABO,
∴OP=OA,∠POC=∠AOB
∴∠AOP=∠BOC-∠AOB+∠POC=∠BOC=90°,
∴△AOP为等腰直角三角形,
∴∠OAF=45°,是定值,不发生改变.
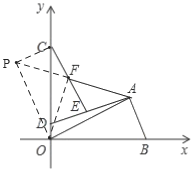
(3)过N作NP∥MB,交X轴于P;连接NQ、MQ、BQ、B′Q,
由(1)得△BOC是等腰直角三角形
∵B、B′关于y轴对称,
∴BB′=2OB,BC=B′C,
∴△BCB′是等腰直角三角形,∠BB′C=∠B′BC=45°,
∵NP∥MB,
∴∠B′PN=∠B′BC=45°,
∵∠PB′N=∠BB′C=45°,
∴∠B′PN=∠PB′N,
∴NP=NB′=MB
在△PTN和△BTM中,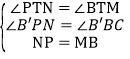 ,
,
∴△PTN≌△BTM,NT=MT,T为MN中点,
∵QT⊥MN,
∴QT为MN垂直平分线,
∴MQ=NQ
∵B、B′关于y轴对称,Q在y轴上,
∴BQ=B′Q
在△BQM≌△B′QN中,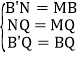 ,
,
∴△BQM≌△B′QN(SSS),
∴∠NB′Q=∠MBQ,
在△BCQ和△B′CQ中,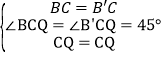
∴△BCQ≌△B′CQ,
∴∠MBQ=∠CB′Q=∠NB′Q,
∵∠CB′Q+∠NB′Q=180°,
∴∠NB′Q=∠MBQ=90°,
∴∠OBQ=45°,
∴△OBQ为等腰直角三角形,
∴OQ=OB=t
∴Q(0,-t).


科目:初中数学 来源: 题型:
【题目】如图,A、B两点分别位于一个池塘的两端,小明想用绳子测量A、B间的距离,但绳子不够长.他叔叔帮他出了一个这样的主意:先在地上取一个可以直接到达A点和B点的点C,连接AC并延长到D,使CD=AC;连接BC并延长到E,使CE=CB;连接DE并测量出它的长度.
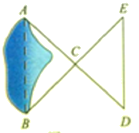
(1)DE=AB吗?请说明理由;
(2)如果DE的长度是8 m,则AB的长度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,OB和OC分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若DE=5,BD=3,则线段CE的长为( )
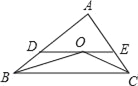
A. 3 B. 1 C. 2 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,D是边AC上的一点,连接BD,使∠A=2∠1,E是BC上的一点,以BE为直径的⊙O经过点D.

(1)求证:AC是⊙O的切线;
(2)若∠A=60°,⊙O的半径为2,求阴影部分的面积.(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,点![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点.求线段
的中点.求线段![]() 的长;
的长;

(2)点![]() 在线段
在线段![]() 上,若
上,若![]() ,点
,点![]() ,
,![]() 分别是线段
分别是线段![]() ,
,![]() 的中点.你能得出
的中点.你能得出![]() 的长度吗?并说明理由.
的长度吗?并说明理由.
(3)类似的,如图2,![]() 是直角,射线
是直角,射线![]() 在
在![]() 外部,且
外部,且![]() 是锐角,
是锐角,![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 的平分线.当
的平分线.当![]() 的大小发生改变时,
的大小发生改变时,![]() 的大小也会发生改变吗?为什么?
的大小也会发生改变吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:在用尺规作线段![]() 等于线段
等于线段![]() 时,小明的具体做法如下:
时,小明的具体做法如下:
已知:如图,线段![]() .
.![]()
求作:线段![]() ,使得线段
,使得线段![]() .
.
作法: ① 作射线![]() ;
;
② 在射线![]() 上截取
上截取![]() .
.
∴线段![]() 为所求.
为所求.
![]()
解决下列问题:
已知:如图,线段![]() .
.![]()
(1)请你仿照小明的作法,在上图中的射线![]() 上作线段
上作线段![]() ,使得
,使得![]() ;(不要求写作法和结论,保留作图痕迹)
;(不要求写作法和结论,保留作图痕迹)
(2)在(1)的条件下,取![]() 的中点
的中点![]() .若
.若![]() ,求线段
,求线段![]() 的长.(要求:第(2)问重新画图解答)
的长.(要求:第(2)问重新画图解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,过点
,过点![]() 画
画![]() 轴的垂线
轴的垂线![]() ,点
,点![]() 在线段
在线段![]() 上,连结
上,连结![]() 并延长交直线
并延长交直线![]() 于点
于点![]() ,过点
,过点![]() 画
画![]() 交直线
交直线![]() 于点
于点![]() .
.
(1)求![]() 的度数,并直接写出直线
的度数,并直接写出直线![]() 的解析式;
的解析式;
(2)若点![]() 的横坐标为2,求
的横坐标为2,求![]() 的长;
的长;
(3)当![]() 时,求点
时,求点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们常用的数是十进制,十进制数要用10个数码:0,1,2,3,4,5,6,7,8,9如十进制3245=3×103+2×102+4×101+5×100在电子计算机中用的是二进制,只要2个数码:0和1.如二进制110=1×22+1×21+0×20,相当于十进制数中的6;二进制110101=1×25+1×24+0×23+1×22+0×21+1×20,相当于十进制数中的53.(注意:非零有理数的零次幂都为1即a°=(a≠0))
(1)二进制中的1011等于十进制中的数是_____;
(2)十进制中的100等于二进制中的数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
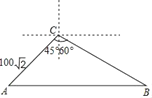
【题目】在某校组织的“交通安全宣传教育月”活动中,八年级数学兴趣小组的同学进行了如下的课外实践活动.具体内容如下:在一段笔直的公路上选取两点A、B,在公路另一侧的开阔地带选取一观测点C,在C处测得点A位于C点的南偏西45°方向,且距离为100![]() 米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒,请你帮助他们算一算,这辆小车是否超速?(参考数据:
米,又测得点B位于C点的南偏东60°方向.已知该路段为乡村公路,限速为60千米/时,兴趣小组在观察中测得一辆小轿车经过该路段用时13秒,请你帮助他们算一算,这辆小车是否超速?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,计算结果保留两位小数)
≈1.73,计算结果保留两位小数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com