
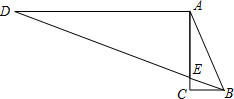
 如图,AD∥BC,AC⊥BC于C,BD和AC相交于E,且DE=2AB,若∠BAC=21°,则∠DBC=
如图,AD∥BC,AC⊥BC于C,BD和AC相交于E,且DE=2AB,若∠BAC=21°,则∠DBC= DE,再求出AB=AF,然后根据等边对等角的性质可得∠D=∠DAF,∠AFB=∠ABF,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠AFB=2∠D,根据直角三角形两锐角互余可求出∠ABC,然后求解即可.
DE,再求出AB=AF,然后根据等边对等角的性质可得∠D=∠DAF,∠AFB=∠ABF,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠AFB=2∠D,根据直角三角形两锐角互余可求出∠ABC,然后求解即可.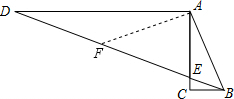 解:如图,取DE的中点F,连接AF,
解:如图,取DE的中点F,连接AF, DE,
DE,

 阅读快车系列答案
阅读快车系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com