练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    直角三角形ABC中，∠ABC=90°，AC=10，BC=6，AB=8。P是AC上的一个动点，当P在AC上运动时，设PC=x，△ABP 的面积为y.

    （1）求AC边上的高是多少？

    （2）求y与x之间的关系式。

     

    【答案】

    （1）4.8；（2）y=-2.4x+24

    【解析】

    试题分析：（1）根据等面积法求解即可；

    （2）作PD⊥AB，可得△ADP∽△ABC，根据相似三角形的性质，可用x表示出PD的长，根据S△ABP=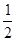AB×PD，代入数值，即可求出y与x之间的关系式．

    解：（1）设AC边上的高是x，由题意得

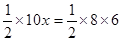
    解得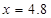

    答：AC边上的高是4.8；

    （2）作PD⊥AB

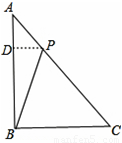
    ∴△ADP∽△ABC，

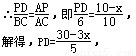
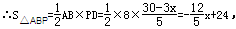
    ∴y与x之间的关系式为：y=-2.4x+24.

    考点：三角形的面积公式，相似三角形的判定和性质

    点评：相似三角形的判定和性质是初中数学的重点，贯穿于整个初中数学的学习，是中考中比较常见的知识点，一般难度不大，需熟练掌握.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网如图，在等腰直角三角形ABC中，∠C=90°，AC=6，D是AC上一点，若tan∠DBA=
    1
    5
    ，则AD的长是（　　）
    A、
    		2
    B、2
    C、1
    D、2
    		2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    精英家教网如图，在直角三角形ABC中，∠C=90°，AB=5，AC=3．点P、Q分别是BC边和AB边上的动点，点P从点C向点B运动，点Q从点A向点B运动，QR⊥BC，垂足为R，设P、Q同时运动，并且当P运动4x单位长度时，Q运动5（1-x）单位长度．是否存在x的值，使以P、Q、R为顶点的三角形与△ACP相似？若存在，求出所有x的值；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在直角三角形ABC中，∠C=90°，三内角∠A，∠B，∠C的对边分别是a，b，c，若a=15，c=25，则b=
    20
    20
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，等腰直角三角形ABC中，∠BAC=90°，D、E分别为AB、AC边上的点，AD=AE，AF⊥BE交BC于点F，过点F作FG⊥CD交BE的延长线于点G，交AC于点M．
    （1）求证：△ADC≌△AEB；
    （2）判断△EGM是什么三角形，并证明你的结论；
    （3）判断线段BG、AF与FG的数量关系并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，直角三角形ABC中，∠ABC=90°，点D、E分别是AC、BC的中点，AB=3，BC=4，则DE和BD的长分别为（　　）

    查看答案和解析>>

    同步练习册答案