
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD,AC分别交于点E,F,且∠ACB=∠DCE. 
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB= ![]() ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.
【答案】
(1)解:直线CE与⊙O相切.
理由如下:
∵四边形ABCD是矩形,
∴BC∥AD,∠ACB=∠DAC;
又∵∠ACB=∠DCE,
∴∠DAC=∠DCE;
连接OE,则∠DAC=∠AEO=∠DCE;
∵∠DCE+∠DEC=90°
∴∠AE0+∠DEC=90°
∴∠OEC=90°,即OE⊥CE.
又OE是⊙O的半径,
∴直线CE与⊙O相切
(2)解:∵tan∠ACB= ![]() =
= ![]() ,BC=2,
,BC=2,
∴AB=BCtan∠ACB= ![]() ,
,
∴AC= ![]() ;
;
又∵∠ACB=∠DCE,
∴tan∠DCE=tan∠ACB= ![]() ,
,
∴DE=DCtan∠DCE=1;
方法一:在Rt△CDE中,CE= ![]() =
= ![]() ,
,
连接OE,设⊙O的半径为r,则在Rt△COE中,CO2=OE2+CE2,即 ![]() =r2+3
=r2+3
解得:r= ![]()
方法二:AE=AD﹣DE=1,过点O作OM⊥AE于点M,则AM= ![]() AE=
AE= ![]()
在Rt△AMO中,OA= ![]() =
= ![]() ÷
÷ ![]() =
= ![]()

【解析】(1)连接OE.欲证直线CE与⊙O相切,只需证明∠CEO=90°,即OE⊥CE即可;(2)在直角三角形ABC中,根据三角函数的定义可以求得AB= ![]() ,然后根据勾股定理求得AC=
,然后根据勾股定理求得AC= ![]() ,同理知DE=1; 方法一、在Rt△COE中,利用勾股定理可以求得CO2=OE2+CE2 , 即
,同理知DE=1; 方法一、在Rt△COE中,利用勾股定理可以求得CO2=OE2+CE2 , 即 ![]() =r2+3,从而易得r的值;
=r2+3,从而易得r的值;
方法二、过点O作OM⊥AE于点M,在Rt△AMO中,根据三角函数的定义可以求得r的值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知,如图,AB和DE是直立在地面上的两根立柱,AB=5m,某一时刻AB在阳光下的投影BC=3m. 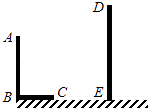
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,下列说法中不正确的是( ) 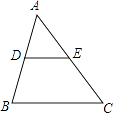
A.DE= ![]() BC
BC
B.![]()
C.△ADE∽△ABC
D.S△ADE:S△ABC=1:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点,EF与BD交于点H. 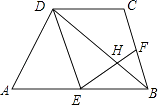
(1)求证:△EDH∽△FBH;
(2)若BD=6,求DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,点D是BC边上的一动点(不与B、C重合),∠ADE=∠B=∠α,DE交AB于点E,且tan∠α= ![]() ,有以下的结论:①△DBE∽△ACD;②△ADE∽△ACD;③△BDE为直角三角形时,BD为8或
,有以下的结论:①△DBE∽△ACD;②△ADE∽△ACD;③△BDE为直角三角形时,BD为8或 ![]() ;④0<BE≤5,其中正确的结论是(填入正确结论的序号)
;④0<BE≤5,其中正确的结论是(填入正确结论的序号) 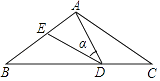
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系中,已知点A(﹣2,0),B(0,4),C(0,3),过点C作直线交x轴于点D,使得以D,O,C为顶点的三角形与△AOB相似,求点D的坐标. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旅游公司在景区内配置了50辆观光车供游客租赁使用,假定每辆观光车一天内最多能出租一次,且每辆车的日租金x(元)是5的倍数,发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆,已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)设每日净收入为w元,请写出w与x之间的函数关系式;
(3)若某日的净收入为4420元,且使游客得到实惠,则当天的观光车的日租金是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com