
【题目】如图,在四边形ABCD中,AB∥CD,且AB=2CD,E,F分别是AB,BC的中点,EF与BD交于点H. 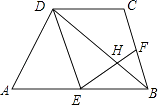
(1)求证:△EDH∽△FBH;
(2)若BD=6,求DH的长.
【答案】
(1)证明:∵在四边形ABCD中,AB∥CD,且AB=2CD,E,是AB的中点,
∴DC= ![]() AB=EB,DC∥BE,
AB=EB,DC∥BE,
∴四边形DCBE是平行四边形,
∴FB∥DE,
∴△EDH∽△FBH
(2)解:由(1)知,BC∥DE,BC=DE,
∵FB= ![]() BC,
BC,
∴FB= ![]() DE.
DE.
∵△EDH∽△FBH,
∴ ![]() =2.
=2.
∵DH+HB=6,
∴DH=4
【解析】(1)先根据题意得出四边形DCBE是平行四边形,再由平行四边形的性质得出FB∥DE,故可得出∠FBH=∠EDH,∠DEH=∠BFH,进而可得出结论;(2)先有平行四边形的性质得出BC∥DE,BC=DE,再由△EDH∽△FBH可得出结论.
【考点精析】掌握三角形中位线定理和相似三角形的判定与性质是解答本题的根本,需要知道连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】某校260名学生参加植树活动,要求每人植4﹣7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵,将各类的人数绘制成扇形图(如图(1))和条形图(如图(2)),经确认扇形图是正确的,而条形图尚有一处错误. 回答下列问题: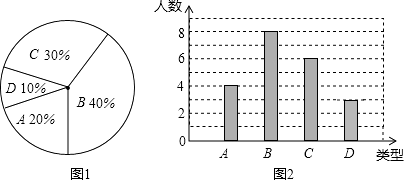
(1)写出条形图中存在的错误,并说明理由;
(2)写出这20名学生每人植树量的众数、中位数;
(3)在求这20名学生每人植树量的平均数时,小宇是这样分析的: 第一步:求平均数的公式是 ![]() =
= ![]() ;
;
第二步:在该问题中,n=4,x1=4,x2=5,x3=6,x4=7;
第三步: ![]() =
= ![]() =5.5(份)
=5.5(份)
①小宇的分析是从哪一步开始出现错误的?
②请你帮他计算出正确的平均数,并估计这260名学生共植树多少棵.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AE是弦,直线CG与⊙O相切于点C,CG∥AE,CG与BA的延长线交于点G,过点C作CD⊥AB于点D,交AE于点F. 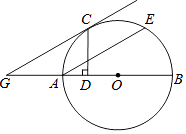
(1)求证: ![]() ;
;
(2)若∠EAB=30°,CF=a,写出求四边形GAFC周长的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点O在对角线AC上,以OA的长为半径的圆O与AD,AC分别交于点E,F,且∠ACB=∠DCE. 
(1)判断直线CE与⊙O的位置关系,并证明你的结论;
(2)若tan∠ACB= ![]() ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AD=3,CD=4,点E在边CD上,且DE=1.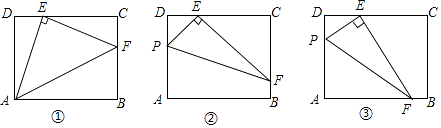
(1)感知:如图①,连接AE,过点E作EF⊥AE,交BC于点F,连接AF,易证:△ADE≌△ECF(不需要证明);
(2)探究:如图②,点P在矩形ABCD的边AD上(点P不与点A、D重合),连接PE,过点E作EF⊥PE,交BC于点F,连接PF.求证:△PDE∽△ECF;
(3)应用:如图③,若EF交AB边于点F,其他条件不变,且△PEF的面积是3,则AP的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】父亲节快到了,明明准备为爸爸煮四个大汤圆作早点:一个芝麻馅,一个水果馅,两个花生馅,四个汤圆除内部馅料不同外,其它一切均相同.
(1)求爸爸吃前两个汤圆刚好都是花生馅的概率;
(2)若给爸爸再增加一个花生馅的汤圆,则爸爸吃前两个汤圆都是花生馅的可能性是否会增大?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com