Question

7．在△ABC中，AB=AC，点D是直线BC上一点（不与B，C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连结CE．
（1）如图1，当点D在线段BC上时，如果∠BAC=90°，则∠BCE=90°°．
（2）设∠BAC=α，∠BCE=β．
①如图2，当点D在线段BC上移动时，α，β之间有怎样的数量关系？请说明理由．
②当点D在直线BC上移动时，α，β之间有怎样的数量关系？请你在备用图上画出图形，并直接写出你的结论．

Answer 1

分析 （1）先用等式的性质得出∠CAE=∠BAD，进而得出△ABD≌△ACE，有∠B=∠ACE，最后用等式的性质即可得出结论；
（2）①由（1）的结论即可得出α+β=180°；
②同（1）的方法即可得出结论．

解答 解：（1）∵∠DAE=∠BAC，∠BAC=∠BAD+∠DAC=∠EAC+∠DAC；
∴∠CAE=∠BAD；
在△ABD和△ACE中，$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$
∴△ABD≌△ACE（SAS）；
∴∠B=∠ACE；
∴∠BCE=∠BCA+∠ACE=∠BCA+∠B=180°-∠BAC=90°；
故答案为90°；
（2）①由（1）中可知β=180°-α，
∴α、β存在的数量关系为α+β=180°；
②当点D在射线BC上时，如图1，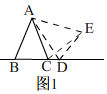

同（1）的方法即可得出，△ABD≌△ACE（SAS）；
∴∠ABD=∠ACE，
∴β=∠BCE=∠ACB+∠ACE=∠ACB+∠ABD=180°-∠BAC=180°-α，
∴α+β=180°；
当点D在射线BC的反向延长线上时，如图2，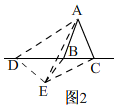

同（1）的方法即可得出，△ABD≌△ACE（SAS）；
∴∠ABD=∠ACE，
∴β=∠BCE=∠ACE-∠ACB=∠ABD-∠ACB=∠BAC=α，
∴α=β．

点评 此题是作图---复杂作图，主要考查了等式的性质，全等三角形的判定，解本题的关键是得出△ABD≌△ACE．