
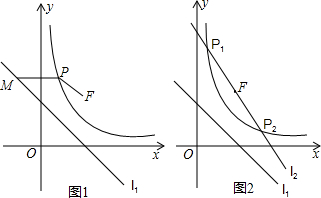
���� ��1����ֱ��l1��y=-x+n����A��-1��3����˫����C��y=$\frac{m}{x}$��x��0��������B��1��2�������ô���ϵ�����������ֱ��l1��˫����C�Ľ���ʽ���ɶ�ֱ��l2��y=kx-2k+2���䷽������ö���F�����ꣻ
��2��������˫����C����ȡһ��P��x��y������P��x���ƽ���߽�ֱ��l1��M��x0��y��������PF��Ȼ��ֱ����PM��PF�ij����̶�֤�ý��ۣ�
��3�����ȹ�P1�ֱ���P1M1��x�ύl1��M1����P1N1��l1������ΪN1����P2�ֱ���P2M2��x�ύl1��M2����P2N2��l1������ΪN2����֤��EF��l1���ɵ�P1N1��EF��P2N2���̶�֤�á�P1N1E�ס�P2N2E��Ȼ�������������εĶ�Ӧ����ȣ�֤�ý��ۣ�
��� ��1���⣺��ֱ��l1��y=-x+n����A��-1��3����
��-��-1��+n=3��
��ã�n=2��
��ֱ��l1�Ľ���ʽΪ��y=-x+2��
��˫����C��y=$\frac{m}{x}$��x��0������B��1��2����
��m=xy=1��2=2��
��˫����C�Ľ���ʽΪ��y=$\frac{2}{x}$��
�߶�ֱ��l2��y=kx-2k+2=k��x-2��+2��
���kΪ�κθ���ʱ����x=2ʱ����y=2��
����ֱ��l2��y=kx-2k+2�������F��2��2����
��2��֤������ͼ1����˫����C����ȡһ��P��x��y������P��x���ƽ���߽�ֱ��l1��M��x0��y��������PF��
��PF=x-x0��
�֡�M��x0��y����ֱ��l1�ϣ�
��-x0+2=y��
��x0=2-y=2-$\frac{2}{x}$��
��PM=x+$\frac{2}{x}$-2��
�֡�PF=$\sqrt{��x-2��^{2}+��y-2��^{2}}$=$\sqrt{��x-2��^{2}+��\frac{2}{x}-2��^{2}}$=$\sqrt{��x+\frac{2}{x}��^{2}-4��x+\frac{2}{x}��+4}$=$\sqrt{��x+\frac{2}{x}-2��^{2}}$=x+$\frac{2}{x}$-2��
��ע��x+$\frac{2}{x}$-2=��$\sqrt{x}$��2+��$\sqrt{\frac{2}{x}}$��2-2$\sqrt{x}$•$\sqrt{\frac{2}{x}}$+2$\sqrt{2}$-2=��$\sqrt{x}$-$\sqrt{\frac{2}{x}}$��2+2$\sqrt{2}$-2=��$\sqrt{x}$-$\sqrt{\frac{2}{x}}$��2+2��$\sqrt{2}$-1����2��$\sqrt{2}$-1����0��
��PM=PF��
��3��֤������ͼ2����P1�ֱ���P1M1��x�ύl1��M1����P1N1��l1������ΪN1����P2�ֱ���P2M2��x�ύl1��M2����P2N2��l1������ΪN2�� ��ֱ��l1�Ľ���ʽΪy=-x+2��
��ֱ��l1�Ľ���ʽΪy=-x+2��
���P1M1N1�͡�P2M2N2���ǵ���ֱ�������Σ�
��P1N1=$\frac{\sqrt{2}}{2}$P1M1=$\frac{\sqrt{2}}{2}$P1F��P2N2=$\frac{\sqrt{2}}{2}$P2M2=$\frac{\sqrt{2}}{2}$P2F��
��ֱ��EF�Ľ���Ϊ��y=x��
��EF��l1��
��P1N1��EF��P2N2��
��$\frac{{N}_{1}E}{E{N}_{2}}=\frac{{P}_{1}F}{F{P}_{2}}$=$\frac{\sqrt{2}{P}_{1}{N}_{1}}{\sqrt{2}{P}_{2}{N}_{2}}$=$\frac{{P}_{1}{N}_{1}}{{P}_{2}{N}_{2}}$��
��$\frac{{N}_{1}E}{E{N}_{2}}$=$\frac{{P}_{1}{N}_{1}}{{P}_{2}{N}_{2}}$��
���P1N1E�ס�P2N2E��
���P1EN1=��P2EN2��
�ߡ�P1EF=90��-��P1EN1����P2EF=90��-��P2EN2��
���P1EF=��P2EF��
��EFƽ�֡�P1EP2��
���� �������ڷ����������ۺ��⣮�����˴���ϵ����������ʽ�����ɶ���������ֱ�������ε������Լ����������ε��ж������ʣ�ע��ȷ�����������ǽ����Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
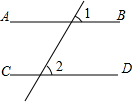 ��ͼ���ɡ�1=��2�õ�AB��CD�������ǣ�������
��ͼ���ɡ�1=��2�õ�AB��CD�������ǣ�������| A�� | ��ֱ��ƽ�У�ͬλ����� | B�� | ��ֱ��ƽ�У��ڴ������ | ||
| C�� | ͬλ����ȣ���ֱ��ƽ�� | D�� | �ڴ�����ȣ���ֱ��ƽ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
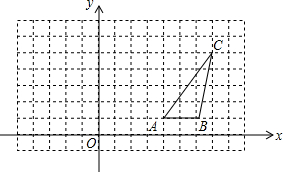 ��ͼ����ABC�Ķ�������ֱ�Ϊ��4��1����B��6��1����C��7��5��
��ͼ����ABC�Ķ�������ֱ�Ϊ��4��1����B��6��1����C��7��5���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
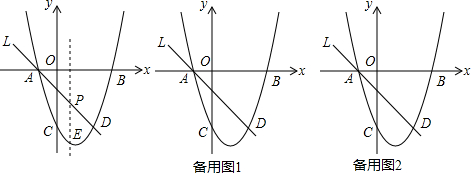
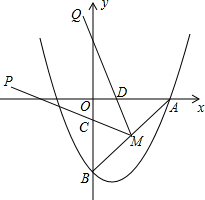 ��ͼ��������y=ax2-2ax-4��x����������ڵ�A����y���ڵ�B����OA=OB��
��ͼ��������y=ax2-2ax-4��x����������ڵ�A����y���ڵ�B����OA=OB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
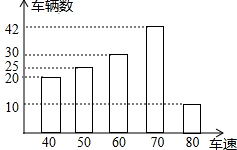 Ϊ�˽�һ·�γ�����ʻ�ٶȵ����������ͳ���˸�·������7��00��9��00���������ij��٣���λ��ǧ��/ʱ���������Ƴ���ͼ��ʾ������ͳ��ͼ����Щ���ٵ�������70ǧ��/ʱ��
Ϊ�˽�һ·�γ�����ʻ�ٶȵ����������ͳ���˸�·������7��00��9��00���������ij��٣���λ��ǧ��/ʱ���������Ƴ���ͼ��ʾ������ͳ��ͼ����Щ���ٵ�������70ǧ��/ʱ���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com