
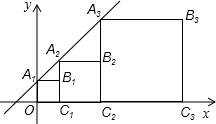
 如图四边形A1B1C1O,A2B2C2C1,A3B3C3C2均为正方形.点A1,A2,A3和点C1,C2,C3分别在直线y=kx+b(k>0)和x轴上,点B3的坐标是(
如图四边形A1B1C1O,A2B2C2C1,A3B3C3C2均为正方形.点A1,A2,A3和点C1,C2,C3分别在直线y=kx+b(k>0)和x轴上,点B3的坐标是( ,
, ),则k+b=
),则k+b= ,
, ),可求得A3的坐标是(
),可求得A3的坐标是( ,
, ),易证得△A2A1B1∽△A3A2B2,然后由相似三角形的对应边成比例,可求得a的值,又由点A1,A2,A3在直线y=kx+b(k>0)上,利用待定系数法即可求得k与b的值,继而求得答案.
),易证得△A2A1B1∽△A3A2B2,然后由相似三角形的对应边成比例,可求得a的值,又由点A1,A2,A3在直线y=kx+b(k>0)上,利用待定系数法即可求得k与b的值,继而求得答案. ,
, ),
), -
- ,
, ),即(
),即( ,
, ),
), -a,A2B1=
-a,A2B1= -a-a=
-a-a= -2a,A3B2=
-2a,A3B2= -(
-( -a)=a-
-a)=a- ,
, k+b=
k+b= ①,
①,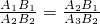 ,
,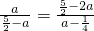 ,
, (舍去),a=1,
(舍去),a=1,

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
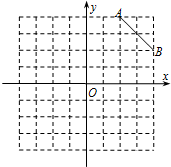 点C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.
点C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图:是规格为8×8的正方形的网格,请你在所给的网格中按下列要求操作:
如图:是规格为8×8的正方形的网格,请你在所给的网格中按下列要求操作:| 10 |
| 2 |
| 10 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
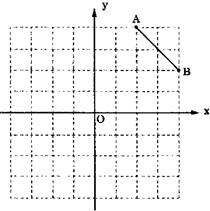
在8×8正方形网格中建立如图的平面直角坐标系,己知A(2,4),B(4,2).
C是第一象限内一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.
1.填空:C点的坐标是_________,△ABC的面积是__________;
2.将△ABC绕点C旋转180°得到△A1B1C,连结AB1,BA1,试判断四边形AB1A1B是何种特殊四边形,请说明理由;
3.请探究:在x轴上是否存在这样的点P,使四边形ABOP的面积等于△ABC面积
2倍.若存在,请直接写出点P的坐标(不必写出解答过程);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2011-2012学年辽宁省九年级下学期第二次模拟考试数学卷(解析版) 题型:解答题
在8×8正方形网格中建立如图的平面直角坐标系,己知A(2,4),B(4,2).
C是第一象限内一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.
1.填空:C点的坐标是_________,△ABC的面积是__________;
2.将△ABC绕点C旋转180°得到△A1B1C,连结AB1,BA1,试判断四边形AB1A1B是何种特殊四边形,请说明理由;
3.请探究:在x轴上是否存在这样的点P,使四边形ABOP的面积等于△ABC面积
2倍.若存在,请直接写出点P的坐标(不必写出解答过程);若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com