
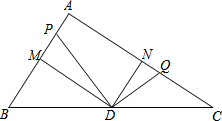
 如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点M、N分别为AB,AC边的中点,点D为BC边的中点,动点P从点A出发,沿射线AB方向移动,作∠PDQ=90°,点Q在AC上,设AP=x,CQ=y.
如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点M、N分别为AB,AC边的中点,点D为BC边的中点,动点P从点A出发,沿射线AB方向移动,作∠PDQ=90°,点Q在AC上,设AP=x,CQ=y.| PM |
| QN |
| DM |
| DN |
| 4 |
| 3 |
| 3 |
| 4 |
| 5 |
| 2 |
| CH |
| CQ |
| PM |
| QN |
| DM |
| DN |
| 4 |
| 3 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 7 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 7 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 7 |
| 4 |
| 3 |
| 4 |
| 7 |
| 4 |
| 25 |
| 3 |
| 25 |
| 3 |
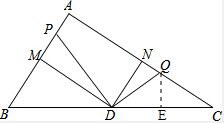
| 25 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 13 |
| 3 |
| 5 |
| 2 |
| CE |
| CQ |
| AC |
| BC |
| 4 |
| 5 |
| CE |
| CQ |
| 4 |
| 5 |
| 5 |
| 4 |
| 25 |
| 8 |
| 3 |
| 4 |
| 7 |
| 4 |
| 25 |
| 8 |
| 11 |
| 6 |
| 25 |
| 3 |
| 13 |
| 3 |
| 11 |
| 6 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| S△ABC |
| S△DEF |
| AB•BC |
| DE•EF |
| S△ABC |
| S△DEF |
| AB•BC |
| DE•EF |
查看答案和解析>>
科目:初中数学 来源: 题型:
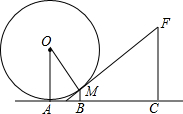 如图,一个小朋友玩“滚铁环”游戏,铁环是圆形的,铁环向前滚动时,铁环与铁钩相切,这个游戏抽象为数学问题,如图,已知铁环的半径为25cm,铁环中心为O,铁环钩与铁环相切点为M,铁环也地面接触点为A,且sin∠MOA=
如图,一个小朋友玩“滚铁环”游戏,铁环是圆形的,铁环向前滚动时,铁环与铁钩相切,这个游戏抽象为数学问题,如图,已知铁环的半径为25cm,铁环中心为O,铁环钩与铁环相切点为M,铁环也地面接触点为A,且sin∠MOA=| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 60.5~70.5 | 3 | a |
| 70.5~80.5 | 6 | 0.12 |
| 80.5~90.5 | 9 | 0.18 |
| 90.5~100.5 | 17 | 0.34 |
| 100.5~110.5 | b | 0.2 |
| 110.5~120.5 | 5 | 0.1 |
| 合 计 | 50 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
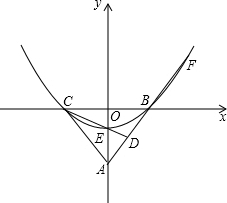 如图,在平面直角坐标系中xoy中,AO=8,AB=AC,sin∠ABC=
如图,在平面直角坐标系中xoy中,AO=8,AB=AC,sin∠ABC=| 4 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com