
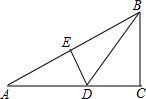
 已知:如图所示,△ABC中,∠C=90°,DE是AB边的中垂线,E为垂足,DE交AC边于点D.若设∠A=x°,∠BDC=y°,
已知:如图所示,△ABC中,∠C=90°,DE是AB边的中垂线,E为垂足,DE交AC边于点D.若设∠A=x°,∠BDC=y°,

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| A、40,50 |
| B、45,50 |
| C、50,50 |
| D、50,70 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
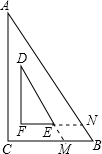 如图,是一块学生用的直角三角板ABC,其中∠A=30°,斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边间的距离都是1cm,延长DE交BC于点M,延长FE交AB于点N.
如图,是一块学生用的直角三角板ABC,其中∠A=30°,斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边间的距离都是1cm,延长DE交BC于点M,延长FE交AB于点N.查看答案和解析>>
科目:初中数学 来源: 题型:
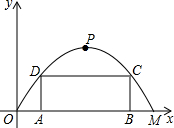 如图,龙丽公路某隧道横截面为抛物线,其最大高度为9米,底部宽度OM为18米. 现以O点为原点,OM所在直线为x轴建立直角坐标系.
如图,龙丽公路某隧道横截面为抛物线,其最大高度为9米,底部宽度OM为18米. 现以O点为原点,OM所在直线为x轴建立直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:
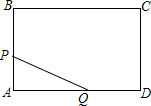 如图,在长方形ABCD中,AB=6cm,BC=8cm,某个时刻点P从A出发,沿着A→B→C在边上运动,速度为1cm/s,与此同时,点Q从D出发,速度为2cm/s,沿着D→A→B→C的方向追点P.
如图,在长方形ABCD中,AB=6cm,BC=8cm,某个时刻点P从A出发,沿着A→B→C在边上运动,速度为1cm/s,与此同时,点Q从D出发,速度为2cm/s,沿着D→A→B→C的方向追点P.| 1 |
| 16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com