

分析 (1)如图1中,由△BDF≌△ADC,可得DF=DC=3,在Rt△BDF中,BD=$\sqrt{B{F}^{2}-D{F}^{2}}$=4,可得AB=$\sqrt{2}$BD=4$\sqrt{2}$;
(2)(2)①由△AOG≌△FOB,推出$\frac{OG}{OB}$=$\frac{OA}{OF}$,推出$\frac{OG}{OA}$=$\frac{OB}{OF}$,又∠BOG=∠AOF,推出△BOG∽△FOA,可得∠BGO=∠OAF=45°;
②如图2中,在AB上截取AM=AG,则∠MGA=∠BGF=45°,推出∠BCM=∠FCA,由BC=$\sqrt{2}$FG,GM=$\sqrt{2}$AC,可得$\frac{BG}{GF}$=$\frac{GM}{GA}$=$\sqrt{2}$,推出△BGM∽△FGA,可得$\frac{BM}{AF}$=$\frac{BG}{GF}$=$\sqrt{2}$,推出BM=$\sqrt{2}$AF,由此即可解决问题;
解答 (1)解:如图1中,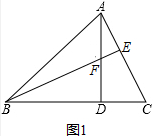
∵∠ABC=45°,AD⊥BC,
∴∠ADB=90°,△ADB是等腰直角三角形,
∴AD=BD,
∵BE⊥AC,
∴∠AEF=∠BDF=90°,
∵∠AFE=∠BFD,
∴∠EAF=∠FBD,∵∠BDF=∠ADC=90°,
∴△BDF≌△ADC,
∴DF=DC=3,
在Rt△BDF中,BD=$\sqrt{B{F}^{2}-D{F}^{2}}$=4,
∴AB=$\sqrt{2}$BD=4$\sqrt{2}$.
(2)①证明:如图2中,设AB交GF于O.
∵∠GAO=∠OFB=90°,∠AOG=∠BOF,
∴△AOG≌△FOB,
∴$\frac{OG}{OB}$=$\frac{OA}{OF}$,
∴$\frac{OG}{OA}$=$\frac{OB}{OF}$,∵∠BOG=∠AOF,
∴△BOG∽△FOA,
∴∠BGO=∠OAF=45°,
∴∠BGF=45°.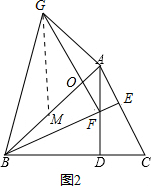
②证明:如图2中,在AB上截取AM=AG,则∠MGA=∠BGF=45°,
∴∠BCM=∠FCA,
∵BC=$\sqrt{2}$FG,GM=$\sqrt{2}$AC,
∴$\frac{BG}{GF}$=$\frac{GM}{GA}$=$\sqrt{2}$,
∴△BGM∽△FGA,
∴$\frac{BM}{AF}$=$\frac{BG}{GF}$=$\sqrt{2}$,
∴BM=$\sqrt{2}$AF,
∴AB=AM+BM=AG+$\sqrt{2}$AF.
点评 本题考查等腰直角三角形的性质和判定、全等三角形的判定和性质.相似三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:填空题
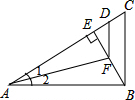 如图,已知:AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则①BF=DF,②DF=BC,③∠ADF=∠C=∠ABE,④FD∥BC,⑤∠CAB=∠CBE=∠DFE,其中正确①④⑤(只填序号).
如图,已知:AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则①BF=DF,②DF=BC,③∠ADF=∠C=∠ABE,④FD∥BC,⑤∠CAB=∠CBE=∠DFE,其中正确①④⑤(只填序号).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
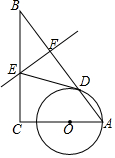 如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.
如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{3}$>-$\frac{1}{4}$ | B. | -|-1|>-|+1| | C. | $\frac{1}{3}$<$\frac{1}{4}$ | D. | |-$\frac{1}{3}$|>|-$\frac{1}{4}$| |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com