
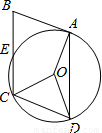
 α=135°,连接OE,由?ABCD可知∠BCD=∠BAD=β,∠B+∠BAD=180°,所以∠BCD=∠OCE+α=β,即β=180°-β+α,整理得:2β=180°+α,再利用已知关系式求出OE∥AB时α的值即可.
α=135°,连接OE,由?ABCD可知∠BCD=∠BAD=β,∠B+∠BAD=180°,所以∠BCD=∠OCE+α=β,即β=180°-β+α,整理得:2β=180°+α,再利用已知关系式求出OE∥AB时α的值即可.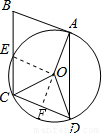
 α=135°,
α=135°, (90°-α),
(90°-α), (90°-α)=135°-
(90°-α)=135°-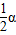 ,
,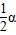 ,可求得α=45°.
,可求得α=45°.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 下垂,如图②,求彩旗下垂时最低处离地面的最小高度h.
下垂,如图②,求彩旗下垂时最低处离地面的最小高度h.查看答案和解析>>
科目:初中数学 来源: 题型:
 18、如图,有一条双向公路隧道,其横断面由抛物线和矩形ABCD的三边DA、AB、BC围成,隧道最大高度为4.9米,AB=10米,BC=2.4米,若有一辆高为4米、宽为2米的集装箱的汽车要通过隧道,为了使箱顶不碰到隧道顶部,又不违反交通规则(汽车应靠道路右侧行驶,不能超过道路中线),汽车的右侧必须离开隧道右壁几米?
18、如图,有一条双向公路隧道,其横断面由抛物线和矩形ABCD的三边DA、AB、BC围成,隧道最大高度为4.9米,AB=10米,BC=2.4米,若有一辆高为4米、宽为2米的集装箱的汽车要通过隧道,为了使箱顶不碰到隧道顶部,又不违反交通规则(汽车应靠道路右侧行驶,不能超过道路中线),汽车的右侧必须离开隧道右壁几米?查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com