
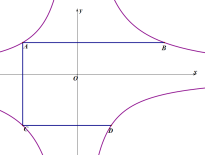
【题目】如图,A、D在反比例函数![]()
![]() 的图像上,点B、C在反比例函数
的图像上,点B、C在反比例函数![]() 的图像上,若AB∥CD∥
的图像上,若AB∥CD∥![]() 轴,
轴,![]() ∥
∥![]() 轴,且
轴,且![]() ,
,![]() ,
,![]() ,则
,则![]() =______.
=______.
【答案】![]()
【解析】
过B点向x轴作垂线,交x轴于点G,过D点向x轴作垂线,交x轴于点H,根据反比例函数系数k的性质可得S矩APOM=S矩ONDH=-m,S矩PCNO=S矩MOGB=n,由此可得S矩APGB=S矩PCDH,由此即可得AP的值,再根据AP的值可得S矩APGB=n-m=4①,S矩PCNO=2S矩APOM即![]() ②,求解即可得出n值.
②,求解即可得出n值.
解:如图,过B点向x轴作垂线,交x轴于点G,过D点向x轴作垂线,交x轴于点H,
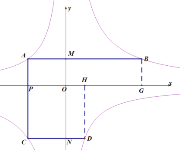
根据反比例函数系数k的性质可得S矩APOM=S矩ONDH=-m,S矩PCNO=S矩MOGB=n,
得S矩APGB=S矩PCDH,
设![]() 则
则![]() ,
,
得![]() ,
,
解得![]() ,
,
可得S矩APGB=n-m=4①,
S矩PCNO=2S矩APOM即![]() ②,
②,
联立①②,解得![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
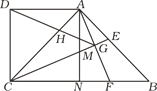
【题目】如图,在四边形ABCD中,AD∥BC,∠BCD=90°,∠ABC=45°,AD=CD,CE平分∠ACB交AB于点E,在BC上截取BF=AE,连接AF交CE于点G,连接DG交AC于点H,过点A作AN⊥BC,垂足为N,AN交CE于点M.则下列结论;①CM=AF;②CE⊥AF;③△ABF∽△DAH;④GD平分∠AGC,其中正确的序号是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
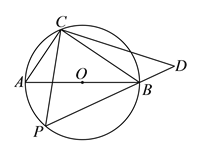
【题目】如图,圆![]() 的直径为
的直径为![]() ,在圆
,在圆![]() 上位于直径
上位于直径![]() 的异侧有定点
的异侧有定点![]() 和动点
和动点![]() ,已知
,已知![]() ,点
,点![]() 在半圆弧
在半圆弧![]() 上运动(不与
上运动(不与![]() 、
、![]() 重合),过
重合),过![]() 作
作![]() 的垂线
的垂线![]() 交
交![]() 的延长线于
的延长线于![]() 点.
点.
(![]() )求证:
)求证: ![]() .
.
(![]() )当点
)当点![]() 运动到
运动到![]() 弧中点时,求
弧中点时,求![]() 的长.
的长.
(![]() )当点
)当点![]() 运动到什么位置时,
运动到什么位置时, ![]() 的面积最大?并求这个最大面积
的面积最大?并求这个最大面积![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某林业部门要考察某种幼树在一定条件下的移植成活率,下图是这种幼树在移植过程中成活情况的一组数据统计结果.下面三个推断:①当移植棵数是1500时,该幼树移植成活的棵数是1356,所以“移植成活”的概率是0.904;②随着移植棵数的增加,“移植成活”的频率总在0.880附近摆动,显示出一定的稳定性,可以估计这种幼树“移植成活”的概率是0.880;③若这种幼树“移植成活”的频率的平均值是0.875,则“移植成活”的概率是0.875.其中合理的是( )

A. ①③B. ②③C. ①D. ②
查看答案和解析>>
科目:初中数学 来源: 题型:
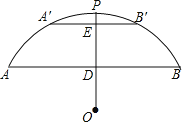
【题目】如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.
(1)求圆弧所在的圆的半径r的长;
(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?
查看答案和解析>>
科目:初中数学 来源: 题型:
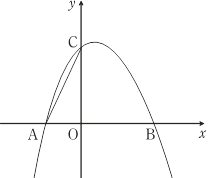
【题目】如图,二次函数y=﹣x2+bx+c的图象与x轴交于点A(﹣1,0),B(2,0),与y轴相交于点C.
(1)求二次函数的解析式;
(2)若点E是第一象限的抛物线上的一个动点,当四边形ABEC的面积最大时,求点E的坐标,并求出四边形ABEC的最大面积;
(3)若点M在抛物线上,且在y轴的右侧.⊙M与y轴相切,切点为D.以C,D,M为顶点的三角形与△AOC相似,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知购买1个足球和1个篮球共需150元,购买2个足球和1个篮球共需200元.
(1)求每个足球和每个篮球的售价;
(2)如果某校计划购买这两种球共50个,总费用不超过4000元,最多可以买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B>90°,CD为∠ACB的角平分线,在AC边上取点E,使DE=DB,且∠AED>90°.若∠A=α,∠ACB=β,则( )

A.∠AED=180°﹣α﹣βB.∠AED=180°﹣α﹣![]() β
β
C.∠AED=90°﹣α+βD.∠AED=90°+α+![]() β
β
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条公路上顺次有![]() 、
、![]() 、
、![]() 三地,甲、乙两车同时从
三地,甲、乙两车同时从![]() 地出发,分别匀速前柱
地出发,分别匀速前柱![]() 地、
地、![]() 地,甲车到达
地,甲车到达![]() 地停留一段时间后原速原路返回,乙车到达
地停留一段时间后原速原路返回,乙车到达![]() 地后立即原速原路返回(掉头时间忽略不计),乙车比甲车早1小时返回
地后立即原速原路返回(掉头时间忽略不计),乙车比甲车早1小时返回![]() 地,甲、乙两车各自行驶的路程
地,甲、乙两车各自行驶的路程![]() (千米)与时间
(千米)与时间![]() (时)(从两车出发时开始计时)之间的变化情况如图所示.
(时)(从两车出发时开始计时)之间的变化情况如图所示.
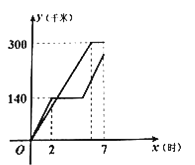
(1)在这个变化过程中,自变量是______,因变量是______.
(2)甲车到达![]() 地停留的时长为______小时,乙车从出发到返回
地停留的时长为______小时,乙车从出发到返回![]() 地共用了______小时.
地共用了______小时.
(3)甲车的速度是______千米/时,乙车的速度是______千米/时.
(4)![]() 、
、![]() 两地相距______千米,甲车返回
两地相距______千米,甲车返回![]() 地途中
地途中![]() 与
与![]() 之间的关系式是______(不必写出自变量取值范围).
之间的关系式是______(不必写出自变量取值范围).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com