
 ,求证:△ABC是“好玩三角形”;
,求证:△ABC是“好玩三角形”; 的值;
的值;
 x,根据条件可以求出AC=2x,由三角函数可以求出BD=2x,从而得出AC=BC,从而得出结论;
x,根据条件可以求出AC=2x,由三角函数可以求出BD=2x,从而得出AC=BC,从而得出结论; ,再分情况讨论就可以求出当AE=PQ时,
,再分情况讨论就可以求出当AE=PQ时, 的值,当AP=QM时,可以求出
的值,当AP=QM时,可以求出 的值;
的值;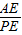 的值就可以求出tanβ的取值范围;
的值就可以求出tanβ的取值范围; ,△APQ为“好玩三角形”的个数为2就是真命题.
,△APQ为“好玩三角形”的个数为2就是真命题.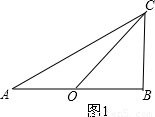
 ,
,
 x,则AC=2x,
x,则AC=2x, AC=x
AC=x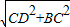 =
=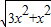 =2x,
=2x,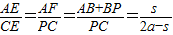 .
.
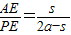 .
. ,
, ,
, MP.
MP.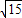 MN,
MN, ,
, =
=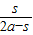 =
=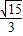 ,
,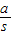 =
=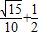
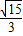 <tanβ<2时,有且只有一个△APQ能成为“好玩三角形”.
<tanβ<2时,有且只有一个△APQ能成为“好玩三角形”.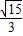 ,
,

科目:初中数学 来源: 题型:
| ||
| 2 |
| a |
| s |
查看答案和解析>>
科目:初中数学 来源:2013年浙江省台州市高级中等学校招生考试数学 题型:044
如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”
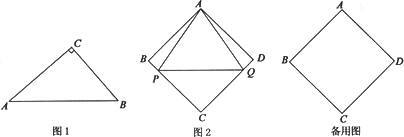
(1)请用直尺与圆规画一个“好玩三角形”;
(2)如图1,在Rt△ABC中,∠C=90°,![]() ,求证:△ABC是“好玩三角形”;
,求证:△ABC是“好玩三角形”;
(3)如图2,已知菱形ABCD的边长为a,∠ABC=2β,点P,Q从点A同时出发,以相同的速度分别沿折线AB-BC和AD-DC向终点C运动,记点P所经过的路程为S
①当β=45°时,若△APQ是“好玩三角形”,试求![]() 的值
的值
②当tanβ的取值在什么范围内,点P,Q在运动过程中,有且只有一个△APQ能成为“好玩三角形”请直接写出tanβ的取值范围.
(4)本小题为选做题
依据(3)中的条件,提出一个关于“在点P,Q的运动过程中,tanβ的取值范围与△APQ是“好玩三角形”的个数关系的真命题(“好玩三角形”的个数限定不能为1).
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(浙江台州卷)数学(带解析) 题型:解答题
如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”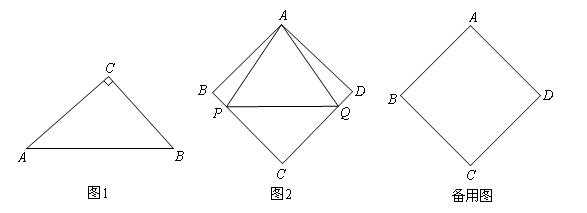
(1)请用直尺与圆规画一个“好玩三角形”;
(2)如图1,在Rt△ABC中,∠C=90°,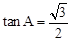 ,求证:△ABC是“好玩三角形”;
,求证:△ABC是“好玩三角形”;
(3)如图2,已知菱形ABCD的边长为a, ∠ABC=2β,点P,Q从点A同时出发,以相同的速度分别沿折线AB-BC和AD-DC向终点C运动,记点P所经过的路程为s
①当β=45°时,若△APQ是“好玩三角形”,试求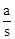 的值;
的值;
②当tanβ的取值在什么范围内,点P,Q在运动过程中,有且只有一个△APQ能成为“好玩三角形”?请直接写出tanβ的取值范围。
(4)本小题为选做题
依据(3)中的条件,提出一个关于“在点P,Q的运动过程中,tanβ的取值范围与△APQ是“好玩三角形”的个数关系”的真命题(“好玩三角形”的个数限定不能为1)。
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(浙江台州卷)数学(解析版) 题型:解答题
如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”
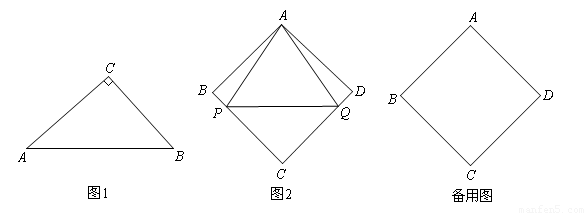
(1)请用直尺与圆规画一个“好玩三角形”;
(2)如图1,在Rt△ABC中,∠C=90°,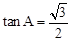 ,求证:△ABC是“好玩三角形”;
,求证:△ABC是“好玩三角形”;
(3)如图2,已知菱形ABCD的边长为a, ∠ABC=2β,点P,Q从点A同时出发,以相同的速度分别沿折线AB-BC和AD-DC向终点C运动,记点P所经过的路程为s
①当β=45°时,若△APQ是“好玩三角形”,试求 的值;
的值;
②当tanβ的取值在什么范围内,点P,Q在运动过程中,有且只有一个△APQ能成为“好玩三角形”?请直接写出tanβ的取值范围。
(4)本小题为选做题
依据(3)中的条件,提出一个关于“在点P,Q的运动过程中,tanβ的取值范围与△APQ是“好玩三角形”的个数关系”的真命题(“好玩三角形”的个数限定不能为1)。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com