
 在?ABCD中,E为AD的中点,则△DEF与△BCF的面积比为( )
在?ABCD中,E为AD的中点,则△DEF与△BCF的面积比为( )| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:$\sqrt{2}$ |
分析 由于四边形ABCD是平行四边形,那么AD∥BC,AD=BC,根据平行线分线段成比例定理的推论可得△DEF∽△BCF,再根据E是AD中点,易求出相似比,从而得到结论.
解答 解:如图所示,
∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△DEF∽△BCF,
∴S△DEF:S△BCF=($\frac{DE}{BC}$)2,
又∵E是AD中点,
∴DE=$\frac{1}{2}$AD=$\frac{1}{2}$BC,
∴DE:BC=DF:BF=1:2,
∴S△DEF:S△BCF=1:4,
故选C.
点评 本题考查了平行四边形的性质、平行线分线段成比例定理的推论、相似三角形的判定和性质.解题的关键是知道相似三角形的面积比等于相似比的平方.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:选择题
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 有一根为0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.1×108 | B. | 21×108 | C. | 2.1×109 | D. | 0.21×1010 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
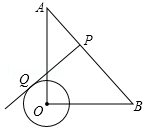 如图,在Rt△AOB中,OA=OB=4$\sqrt{2}$,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线长PQ的最小值为$\sqrt{15}$.
如图,在Rt△AOB中,OA=OB=4$\sqrt{2}$,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线长PQ的最小值为$\sqrt{15}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
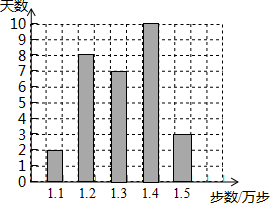 李老师用手机软件记录了某个月(30天)每天走路的步数(单位:万步),她将记录的结果绘制成了如图所示的统计图,在李老师每天走路的步数这组数据中,众数与中位数分别为( )
李老师用手机软件记录了某个月(30天)每天走路的步数(单位:万步),她将记录的结果绘制成了如图所示的统计图,在李老师每天走路的步数这组数据中,众数与中位数分别为( )| A. | 1.2与1.3 | B. | 1.4与1.35 | C. | 1.4与1.3 | D. | 1.3与1.3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.61×103 | B. | 0.161×105 | C. | 1.61×105 | D. | 16.1×104 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com