
【题目】如图,在平面直角坐标系中,直线![]() 与x轴,y轴分别交于点A,B,将
与x轴,y轴分别交于点A,B,将![]() 沿过点A的直线折叠,使点B落在x轴的负半轴上,记作点C,折痕与y轴交于点D,则点D的坐标为______.
沿过点A的直线折叠,使点B落在x轴的负半轴上,记作点C,折痕与y轴交于点D,则点D的坐标为______.

【答案】![]()
【解析】
由条件可先求得A、B坐标.在Rt△AOB中,可求得AB,进而求得OC,设OD=x,则可表示出CD.在Rt△COD中,由勾股定理可列方程,可求得x的值,即可求得D点坐标.
在y![]() x+2
x+2![]() 中,令y=0可求得:x=4,令x=0可求得:y=2
中,令y=0可求得:x=4,令x=0可求得:y=2![]() ,∴A点坐标为(4,0),B点坐标为(0,2
,∴A点坐标为(4,0),B点坐标为(0,2![]() ),∴OA=4,OB=2
),∴OA=4,OB=2![]() .
.
在Rt△AOB中,由勾股定理可得:AB![]() 6,又将△AOB沿过点A的直线折叠B与C重合,∴AC=AB=6,BD=CD,∴OC=AC﹣OA=6﹣4=2.
6,又将△AOB沿过点A的直线折叠B与C重合,∴AC=AB=6,BD=CD,∴OC=AC﹣OA=6﹣4=2.
设OD=x,则BD=CD=2![]() x.
x.
在Rt△OCD中,由勾股定理可得:CD2=OC2+OD2,∴(2![]() x)2=x2+22,解得:x
x)2=x2+22,解得:x![]() ,∴D点坐标为(0,
,∴D点坐标为(0,![]() ).
).
故答案为:(0,![]() ).
).


科目:初中数学 来源: 题型:
【题目】已知二次函数 ![]() (a是常数,
(a是常数, ![]() ),下列结论正确的是( )
),下列结论正确的是( )
A.当a = 1时,函数图像经过点(一1,0)
B.当a = 一2时,函数图像与x轴没有交点
C.若 ![]() ,函数图像的顶点始终在x轴的下方
,函数图像的顶点始终在x轴的下方
D.若 ![]() ,则当
,则当 ![]() 时,y随x 的增大而增大
时,y随x 的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在学习多项式乘以多项式时发现:(![]() x+6)(2x+3)(5x﹣4)的结果是一个多项式,并且最高次项为:
x+6)(2x+3)(5x﹣4)的结果是一个多项式,并且最高次项为:![]() x2x5x=5x3,常数项为:6×3×(﹣4)=﹣72,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是:×3×(﹣4)+2×(﹣4)×6+5×6×3=36,即一次项为36x.认真领会小明同学解决问题的思路,方法,仔细分析上面等式的结构特征.结合自己对多项式乘法法则的理解,解决以下问题.
x2x5x=5x3,常数项为:6×3×(﹣4)=﹣72,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是:×3×(﹣4)+2×(﹣4)×6+5×6×3=36,即一次项为36x.认真领会小明同学解决问题的思路,方法,仔细分析上面等式的结构特征.结合自己对多项式乘法法则的理解,解决以下问题.
(1)计算(x+1)(3x+2)(4x﹣3)所得多项式的一次项系数为 .
(2)(![]() x+6)(2x+3)(5x﹣4)所得多项式的二次项系数为 .
x+6)(2x+3)(5x﹣4)所得多项式的二次项系数为 .
(3)若计算(x2+x+1)(x2﹣3x+a)(2x﹣1)所所得多项式的一次项系数为0,则a= .
(4)若(x+1)2018=a0x2018+a1x2017+a2x2016+a3x2015…+a2017x++a2018,则a2017= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,AB∥CD,∠A=38°,∠C=50°,求∠APC的度数.(提示:作PE∥AB).
(2)如图2,AB∥DC,当点P在线段BD上运动时,∠BAP=∠α,∠DCP=∠β,求∠CPA与∠α,∠β之间的数量关系,并说明理由.
(3)在(2)的条件下,如果点P在段线OB上运动,请你直接写出∠CPA与∠α,∠β之间的数量关系______.
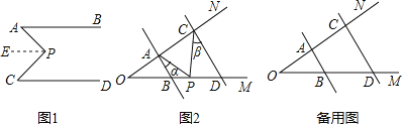
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.现测得AC=50m,BC=100m,∠CAB=120°,请计算A,B两个凉亭之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某童装店有A、B两种型号的童装,其进价与售价如下表所示:
型号 | 进价(元) | 售价(元) |
A型 | 90 | 108 |
B型 | 100 | 130 |
根据市场需要,服装店决定:购进A种服装的数量要比购进B种服装的2倍还多4件,且A种服装购进数量不超过28件,并使这批服装全部销售完毕后的总利润不少于699元.若假设购进B种服装x件,那么:
(1)请写出A、B两种服装全部销售完毕后的总利润y/元用含x/件的式子表示;
(2)请问该服装店有几种满足条件的进货方案?哪种方案获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射击队有甲、乙两名射手,他们各自射击7次,射中靶的环数记录如下:
甲:8,8,8,9,6,8,9
乙:10,7,8,8,5,10,8
(1)分别求出甲、乙两名射手打靶环数的平均数、众数、中位数;
(2)如果要选择一名成绩比较稳定的射手,代表射击队参加比赛,应如何选择?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在小正方形的边长均为1的方格纸中,有线段![]() 和线段
和线段![]() ,点
,点![]() 均在小正方形的顶点上.
均在小正方形的顶点上.
(1)在方格纸中画出以![]() 为斜边的直角三角形
为斜边的直角三角形![]() ,点E在小正方形的顶点上,且
,点E在小正方形的顶点上,且![]() 的面积为5;
的面积为5;
(2)在方格纸中画出以![]() 为一边的
为一边的![]() ,点
,点![]() 在小正方形的顶点上,
在小正方形的顶点上,![]() 的面积为4,射线
的面积为4,射线![]() 与射线
与射线![]() 交于点
交于点![]() ,且
,且![]() ,连接
,连接![]() ,请直接写出线段
,请直接写出线段![]() 的长.
的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com