
 如图,直线L1∥L2,圆O与L1和L2分别相切于点A和点B,点M和点N分别是L1和L2上的动点,MN沿L1和L2平移,圆O的半径为1,∠1=60°,当MN与圆相切时,AM的长度等于$\sqrt{3}$或$\frac{\sqrt{3}}{3}$.
如图,直线L1∥L2,圆O与L1和L2分别相切于点A和点B,点M和点N分别是L1和L2上的动点,MN沿L1和L2平移,圆O的半径为1,∠1=60°,当MN与圆相切时,AM的长度等于$\sqrt{3}$或$\frac{\sqrt{3}}{3}$. 分析 当MN在左侧与⊙O相切时,连接OM、OA,则OM平分∠1,在Rt△OAM中可求得AM;当MN在右侧与⊙O相切时,连接OM、OA,则OM平分∠AMN,在Rt△OAM中可求得MA的长,可求得答案.
解答 解:
当MN在左侧与⊙O相切时,连接OM、OA,如图1,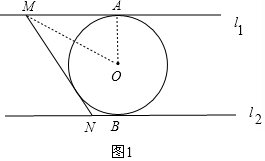
∵MA、MN是⊙O的切线,
∴OM平分∠AMN,OA⊥MA,
∴∠AMO=30°,
∴OM=2OA=2,
在Rt△OAM中,MA=$\sqrt{O{M}^{2}-O{A}^{2}}$=$\sqrt{3}$;
当MN在右侧与⊙O相切时,连接OM、OA,如图2,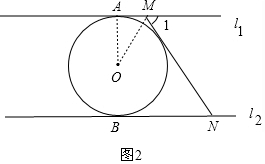
∵∠1=60°,
∴∠AMN=120°,
同上可知∠AMO=$\frac{1}{2}$∠AMN=60°,
∴OM=2AM,
在Rt△OAM中,MA2=OM2-OA2,即MA2=4MA2-1,解得MA=$\frac{\sqrt{3}}{3}$;
综上可知MA的长度为$\sqrt{3}$或$\frac{\sqrt{3}}{3}$,
故答案为:$\sqrt{3}$或$\frac{\sqrt{3}}{3}$.
点评 本题主要考查切线的性质,构造直角三角形,利用勾股定理求线段长度是解题的关键,注意分两种情况讨论.


 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,CD⊥AB,BE⊥AC,垂足分别为点D,点E,BE、CD相交于点O.∠1=∠2,则图中全等三角形共有( )
如图,CD⊥AB,BE⊥AC,垂足分别为点D,点E,BE、CD相交于点O.∠1=∠2,则图中全等三角形共有( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
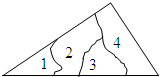 如图,一块三角形玻璃碎成了4块,现在要到玻璃店去配一块与原来的三角形玻璃完全一样的玻璃,那么最省事的办法是带( )去.
如图,一块三角形玻璃碎成了4块,现在要到玻璃店去配一块与原来的三角形玻璃完全一样的玻璃,那么最省事的办法是带( )去.| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com