
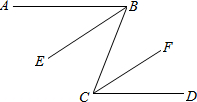
 如图,已知AB∥CD,BE、CF分别平分∠ABC和∠BCD,探索BE与CF的位置关系,并说明理由.
如图,已知AB∥CD,BE、CF分别平分∠ABC和∠BCD,探索BE与CF的位置关系,并说明理由. 分析 根据平行线的性质求出∠ABC=∠BCD,根据角平分线定义得出∠EBC=$\frac{1}{2}$∠ABC∠BCF=$\frac{1}{2}$∠BCD,求出∠EBC=∠BCF,根据平行线的判定得出即可.
解答 解:平行,
理由如下:∵AB∥CD,
∴∠ABC=∠BCD,
∵BE、CF分别平分∠ABC和∠BCD,
∴∠EBC=$\frac{1}{2}$∠ABC∠BCF=$\frac{1}{2}$∠BCD,
∴∠EBC=∠BCF,
∴BE∥CF.
点评 本题考查了平行线的性质和判定,角平分线定义的应用,能求出∠EBC=∠BCF是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.


科目:初中数学 来源: 题型:解答题
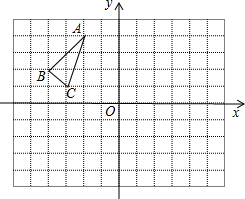 △ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图:
△ABC在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a}{b}$=$\frac{a{c}^{2}}{b{c}^{2}}$ | B. | $\frac{-a-b}{a+b}$=-1 | ||
| C. | $\frac{0.5a+b}{0.2a-0.3b}$=$\frac{5a+10b}{2a-3b}$ | D. | $\frac{a}{b}$=$\frac{a({k}^{2}+1)}{b({k}^{2}+1)}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,3) | B. | (-3,-2) | C. | (-3,2) | D. | (3,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在长为10cm,宽为6cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下的矩形面积是$\frac{108}{5}$cm2.
如图,在长为10cm,宽为6cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下的矩形面积是$\frac{108}{5}$cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com