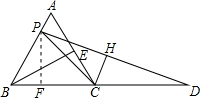
(1)解:过点P作PF⊥BD于点F.
∵AB=BC=2,高BE=

,
∴由锐角三角函数,得∠A=60°,
∴△ABC是等边三角形,
∴∠B=60°,
∴∠BPF=30°.
∵AP=t,
∴PB=2-t,
∴PF=

(2-t),
∴S=

×3×

(2-t),
=-

t+

(0≤t≤2);
(2)证明:∵

,
∴PB=2-

=

,
∴PB=

,PF=
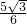
,CF=

,
∴DF=3+

=

,
在Rt△PFD中由勾股定理得
DP=

,
=
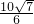
,
在△PCD中

×
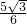
×3=

×
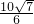
CH,
解得CH=
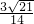
,
K=

=
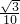
,
∴
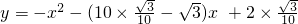
,
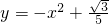
,
当y=0时,解得x=
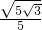
,
∴抛物线与x轴的两个交点坐标分别为:
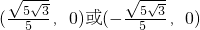
,
∴原二次函数的图象与x轴的交点关于原点对称;
(3)解:不存在正实数P.
∵CH⊥DP,且
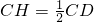
∴∠D=30°
∴DP=2PF=(2-t)

,DF=2-
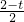
+3=
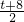
由勾股定理得

解得t
1=7不符合题意应舍去.
t
2=-

不符合题意应舍去.
∴当CH=1.5时,求出的t的值不满足题意要求.
分析:(1)要求s与t的函数关系式,只要表示出DC边上的高就可以了,而CD边上的高可以用三角函数表述出来.因为很容易证明△ABC是正三角形.AP的取值范围是0≤PD≤2.
(2)要求证二次函数与x轴的交点关于原点对称,只要求出抛物线与x轴的交点坐标,要求交点坐标就要求出k值,要求k值就要求出CH、PD的值,可以利用三角形的面积公式和勾股定理求出,从而的解.
(3)当CH=1.5时,利用勾股定理建立方程,从而求出t的值,确定t的值满足不满足题意要求.
点评:本题是一道二次函数的综合试题,考查了求二次函数的解析式,轴对称、三角函数值、勾股定理以及问题的存在性等多个知识点,且计算量比较大,对学生的计算能力有较高的要求.

 ,在BC边的延长线上取一点D,使CD=3.
,在BC边的延长线上取一点D,使CD=3. 时,过点C作CH⊥PD于H,设K=7CH:9PD.求证:关于x的二次函数
时,过点C作CH⊥PD于H,设K=7CH:9PD.求证:关于x的二次函数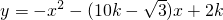 的图象与x轴的两个交点关于原点对称.
的图象与x轴的两个交点关于原点对称.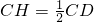 ?如果存在,请求出t的值;如果
?如果存在,请求出t的值;如果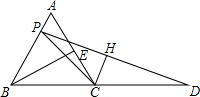 不存在,请说明理由.
不存在,请说明理由. (1)解:过点P作PF⊥BD于点F.
(1)解:过点P作PF⊥BD于点F. ,
, (2-t),
(2-t), ×3×
×3× (2-t),
(2-t), t+
t+ (0≤t≤2);
(0≤t≤2); ,
, =
= ,
, ,PF=
,PF=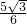 ,CF=
,CF= ,
, =
= ,
, ,
,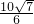 ,
, ×
×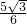 ×3=
×3= ×
×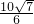 CH,
CH,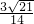 ,
, =
=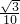 ,
,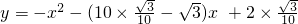 ,
,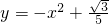 ,
,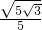 ,
,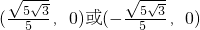 ,
,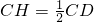
 ,DF=2-
,DF=2-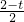 +3=
+3=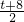

 不符合题意应舍去.
不符合题意应舍去.

 名校课堂系列答案
名校课堂系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为