
【题目】如图所示,∠BAC=90°,AD⊥BC于D,则下列结论中,正确的个数为( ). ①AB⊥AC; ②AD与AC互相垂直; ③点C到AB的垂线段是线段AB; ④点D到BC的距离是线段AD的长度; ⑤线段AB的长度是点B到AC的距离; ⑥线段AB是点B到AC的距离; ⑦AD>BD. 
A.2个
B.4个
C.7个
D.0个
【答案】B
【解析】根据题意,∠BAC=90,所以AB⊥AC,①正确.AD⊥BC于D,所以AD与AC不垂直,②不正确.点到直线的距离为垂线段,所以点C到AB的垂线段是线段AB,③正确.点D到BC的距离应为过D点垂直于AC的垂线段,AD与AC不垂直,所以④错误.因为AB⊥AC,点B到AC的距离为AB,所以⑤⑥正确.AD与BD的具体长度无法推断,所以不能确定二者的大小关系,⑦错误.
【考点精析】本题主要考查了垂线的性质和点到直线的距离的相关知识点,需要掌握垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短;从直线外一点到这条直线的垂线段的长度叫做点到直线的距离才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a、b、c为常数,a≠0)经过点A(﹣1,0),B(5,﹣6),C(6,0).
(a、b、c为常数,a≠0)经过点A(﹣1,0),B(5,﹣6),C(6,0).
(1)求抛物线的解析式;
(2)如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)若点Q为抛物线的对称轴上的一个动点,试指出△QAB为等腰三角形的点Q一共有几个?并请求出其中某一个点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.抛一枚硬币,正面一定朝上
B.掷一颗骰子,朝上一面的点数一定不大于6
C.为了解一种灯泡的使用寿命,宜采用普查的方法
D.“明天的降水概率为80%”,表示明天会有80%的地方下雨
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,要得到△ABD≌△ACD,还需从下列条件中补选一个,则错误的选法是( ) 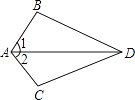
A.AB=AC
B.DB=DC
C.∠ADB=∠ADC
D.∠B=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读下面例题,解答问题;
例题,已知二次三项式x2﹣4x+m有一个因式是(x+3),求另一个因式以及m的值.
解:设另一个因式为(x+n),得x2﹣4x+m=(x+3)(x+n)
则x2﹣4x+m=x2+(n+3)x+3n
∴ ![]()
解得:n=﹣7,m=﹣21
∴另一个因式为(x﹣7),m的值为﹣21
问题:仿照以上方法解答下面问题:
已知二次三项式3x2+5x﹣m有一个因式是(3x﹣1),求另一个因式以及m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,正确的是( )(可以看第4页课本)
A.正整数、负整数和零统称整数
B.正分数、负分数统称有理数
C.零既可以是正整数,也可以是负分数
D.所有的分数都是有理数
查看答案和解析>>
科目:初中数学 来源: 题型:
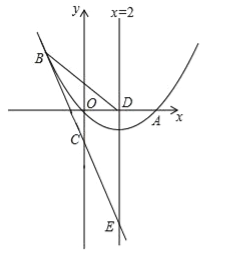
【题目】如图,已知抛物线经过原点o和x轴上一点A(4,0),抛物线顶点为E,它的对称轴与x轴交于点D.直线y=﹣2x﹣1经过抛物线上一点B(﹣2,m)且与y轴交于点C,与抛物线的对称轴交于点F.
(1)求m的值及该抛物线对应的解析式;
(2)P(x,y)是抛物线上的一点,若S△ADP=S△ADC,求出所有符合条件的点P的坐标;
(3)点Q是平面内任意一点,点M从点F出发,沿对称轴向上以每秒1个单位长度的速度匀速运动,设点M的运动时间为t秒,是否能使以Q、A、E、M四点为顶点的四边形是菱形.若能,请直接写出点M的运动时间t的值;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com